Treap

定义

“维护一个有序数列，有插入、删除、查询第 k 大、查询前驱、后继等操作”，对于这种问题，我们常用到二叉排序树（BST，Binary Sort Tree，也称二叉查找树、二叉搜索树）这种数据结构，而 Treap 就是对它的一种优化

有关概念

二叉排序树：一棵有点权的二叉树：若它非空，即有如下性质：对于树上的每个节点，若其左子树非空，则其左子树上的所有节点的值都比这个节点小，且其左子树也是一棵二叉排序树，右子树反之。（当然，左子树大右子树小也是可以的） 二叉排序树有一个性质：其中序遍历一定是有序的。

构造方法

思路

我们发现，在保持树的形态不变的情况下，遇到极端数据，二叉排序树会退化成一条链，复杂度从\(O(logn)\)退化到\(O(n)\)级别，于是对于树上的每个节点，除去原先就有的关键字\(key\)，我们再给它们加上一个随机的值，使这棵树满足堆的性质（但是这棵树并不一定是完全二叉树），称之为优先级\(pri\)，这样能尽量保证这棵树处于平衡状态，不至于退化成一条链。

总的来说就是：

这棵二叉树上的每个节点有两个值，第一个值关键字\(key\)是题目给出的，使这棵树满足排序二叉树的性质，第二个值优先级\(pri\)是随机赋予的，使这棵树满足堆的性质。

另外，对于每一个节点，除了记录其左儿子、右儿子、关键字、优先级之外，可能还要记录\(val\)（该节点关键字出现的次数，用于会多次插入同一关键字的题目）、\(siz\)（该节点及其子树上的节点数目，用于与排名有关的查询操作）。

至于堆是大根堆还是小根堆都无所谓，我这里的各个操作都是基于小根堆。

1. 插入一个数\(k\)。

   首先考虑满足二叉排序树的性质，从根节点开始向下查找，每找到一个节点\(o\)，有如下四种情况：

   (1)\(o\)为空，即创建新节点，初始化，赋\(key\)、\(pri\)值，返回；

   (2)\(k=o.key\)，\(o.val+1\)即可；

   (3)\(k<o.key\)，进入该节点左儿子查找；

   (4)\(k>o.key\)，进入该节点右儿子查找。

   创建完新节点，满足了 BST 的性质，接下来考虑满足堆的性质，介绍如下两种旋转操作：

   

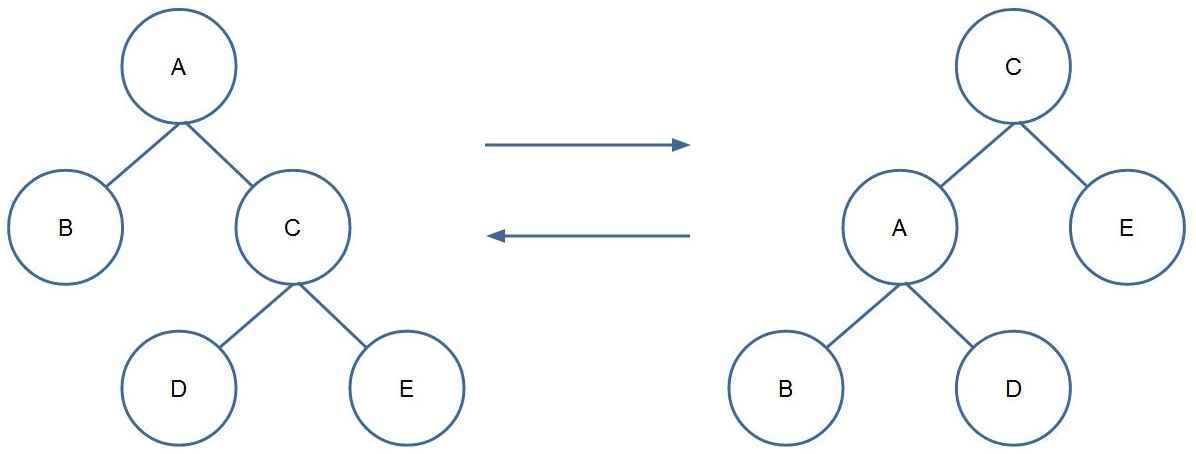
   上图可视为一棵二叉树的一部分，从左图到右图为左旋，反过来为右旋。

   可以看出，旋转前后，这一部分的中序遍历均为\(BADCE\)，即旋转不破坏二叉排序树的性质，于是我们可以利用旋转操作，在保持二叉排序树的前提下，维护堆的性质。

   再具体来讲，这一部分最核心的两个节点是\(A\)和\(C\)，旋转时，只需要调整节点\(D\)的位置，再调整\(A\)、\(C\)的父子关系，最后维护一下\(val\)和\(siz\)值即可。

   在创建完新节点之后，可以得到根节点到这个新节点的一条路径，递归回溯时，对这条路径上的每两个点：若某个左子节点 (\(A\)) 的优先级比其父节点 (\(C\)) 小，则进行一次右旋；若某个右子节点 (\(C\)) 的优先级比其父节点 (\(A\)) 小，则进行一次左旋；这样就完成了插入操作。

   样例推导：（样例中假设已经完成创建新节点，主要演示旋转操作，节点上所示数字为优先级）

   

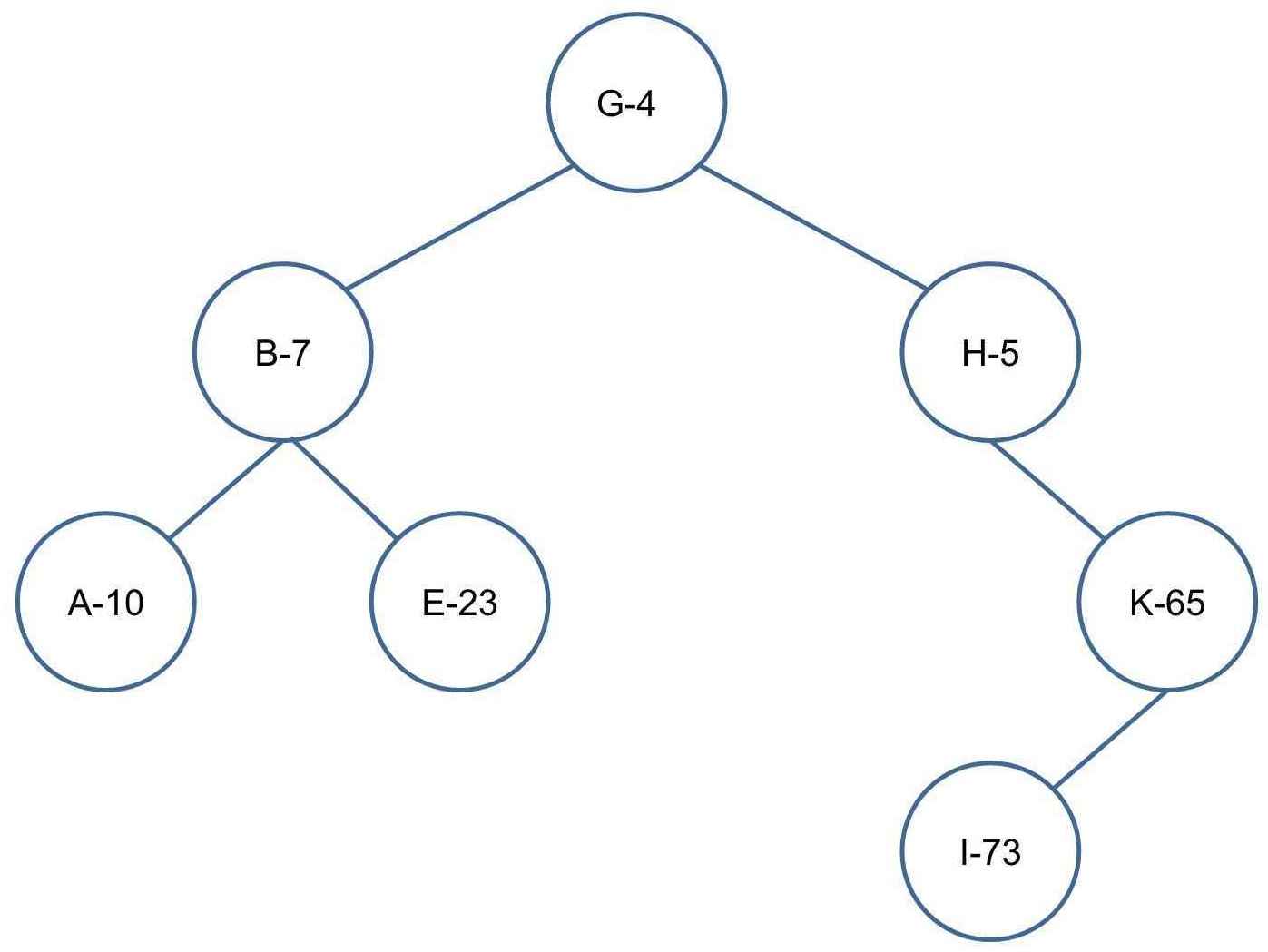
   插入 C-25

   

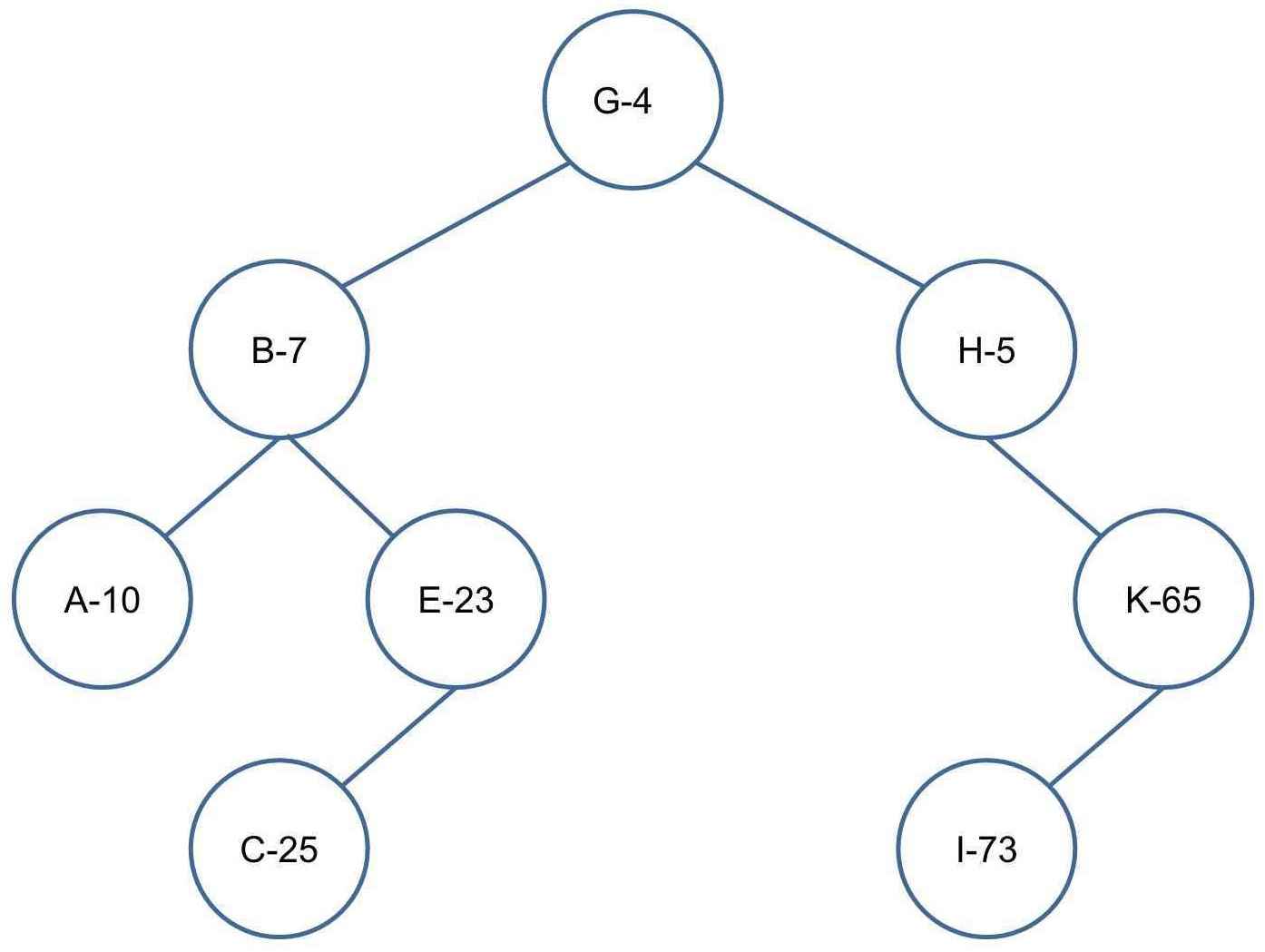
   插入 D-9

   

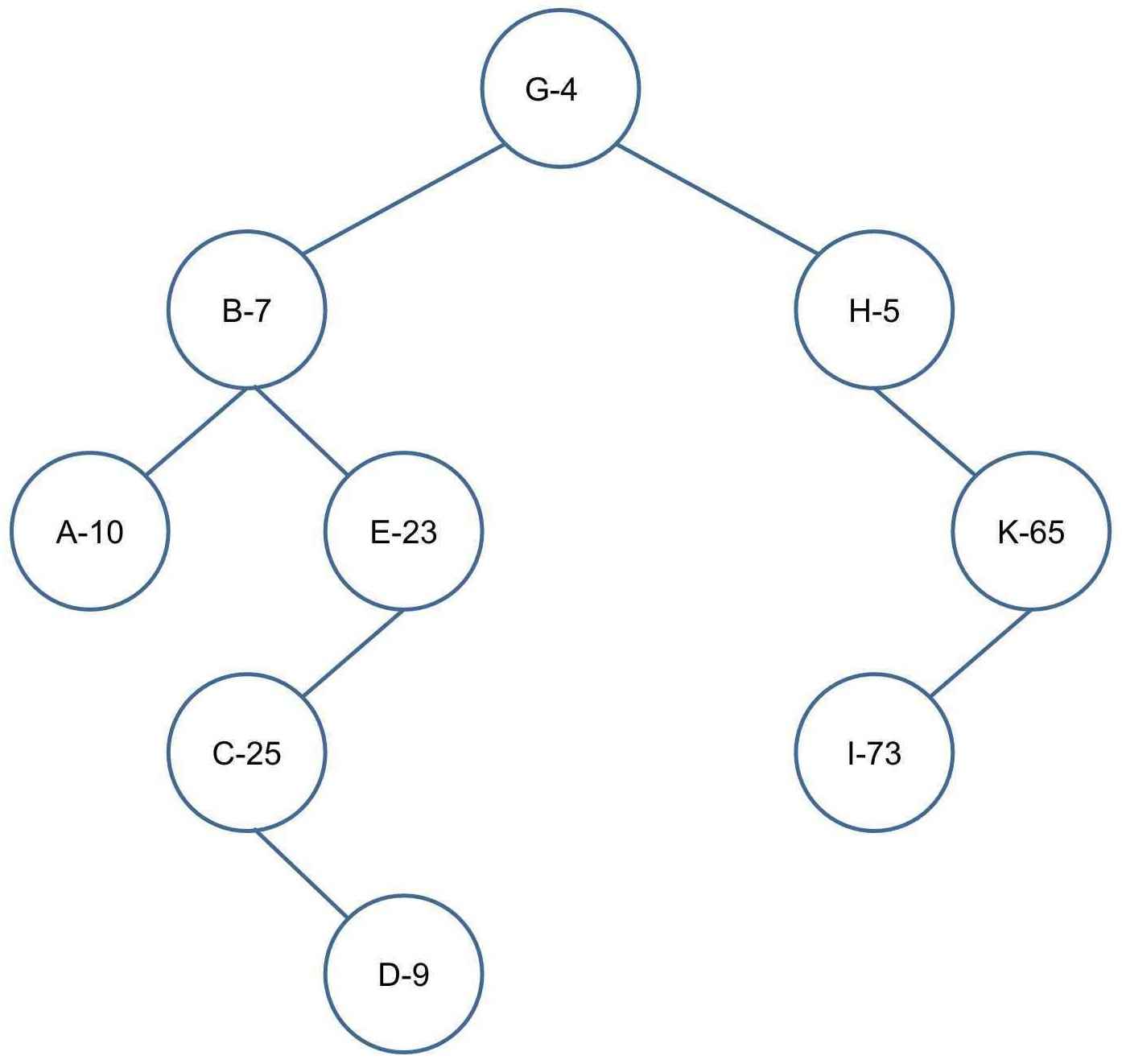
   左旋

   

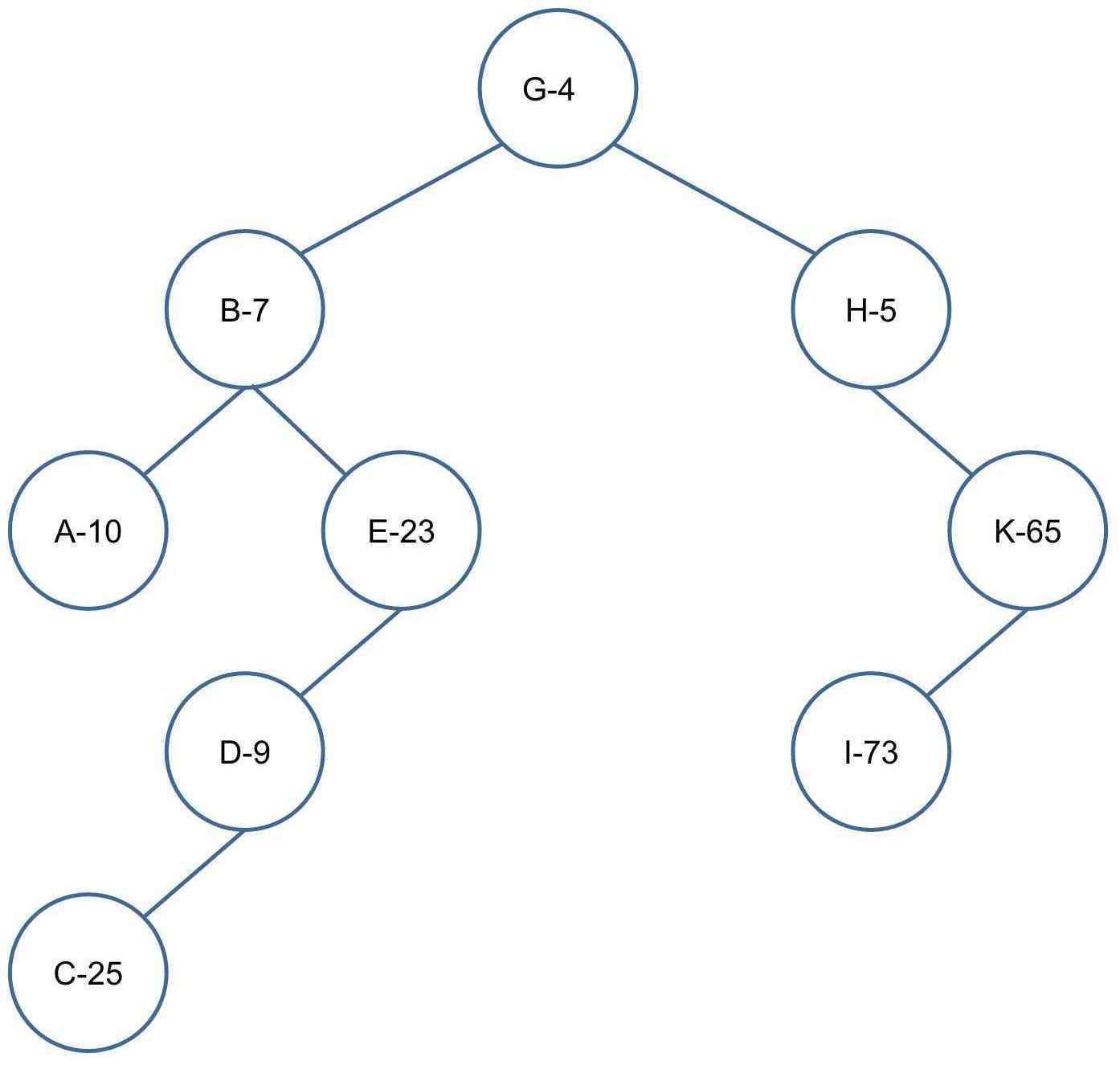
   右旋

   

   插入 F-2

   

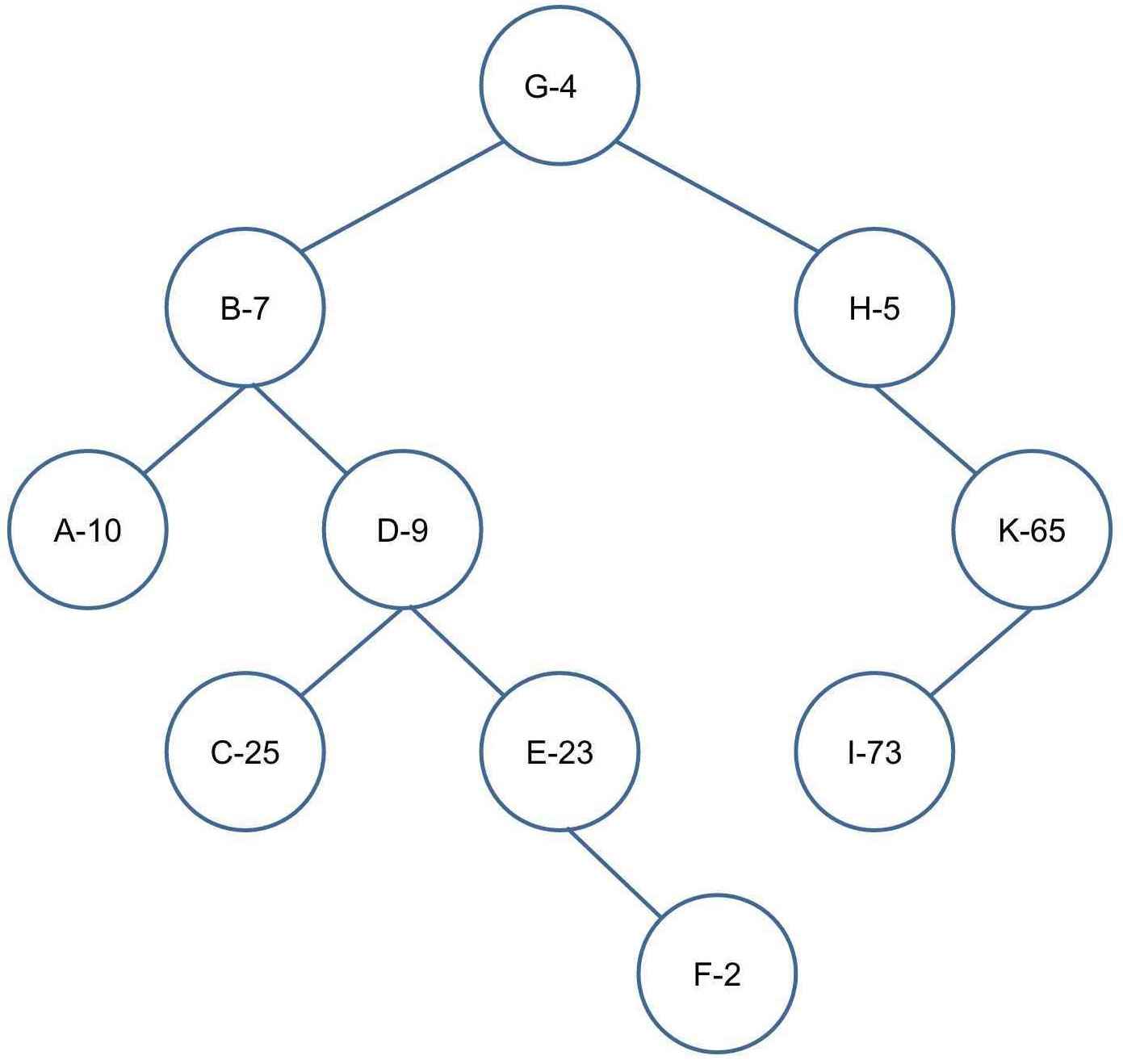
   左旋

   

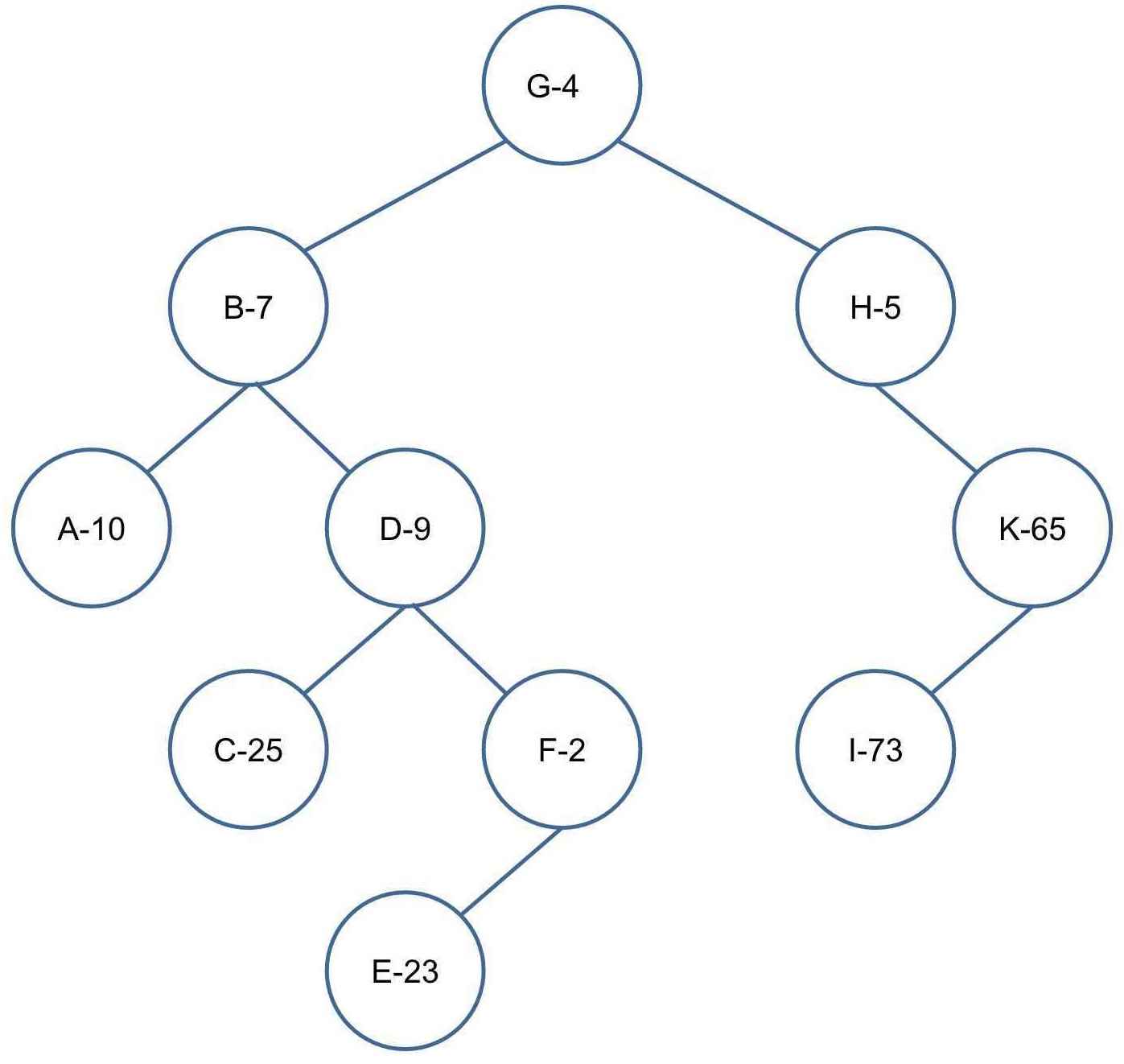
   左旋

   

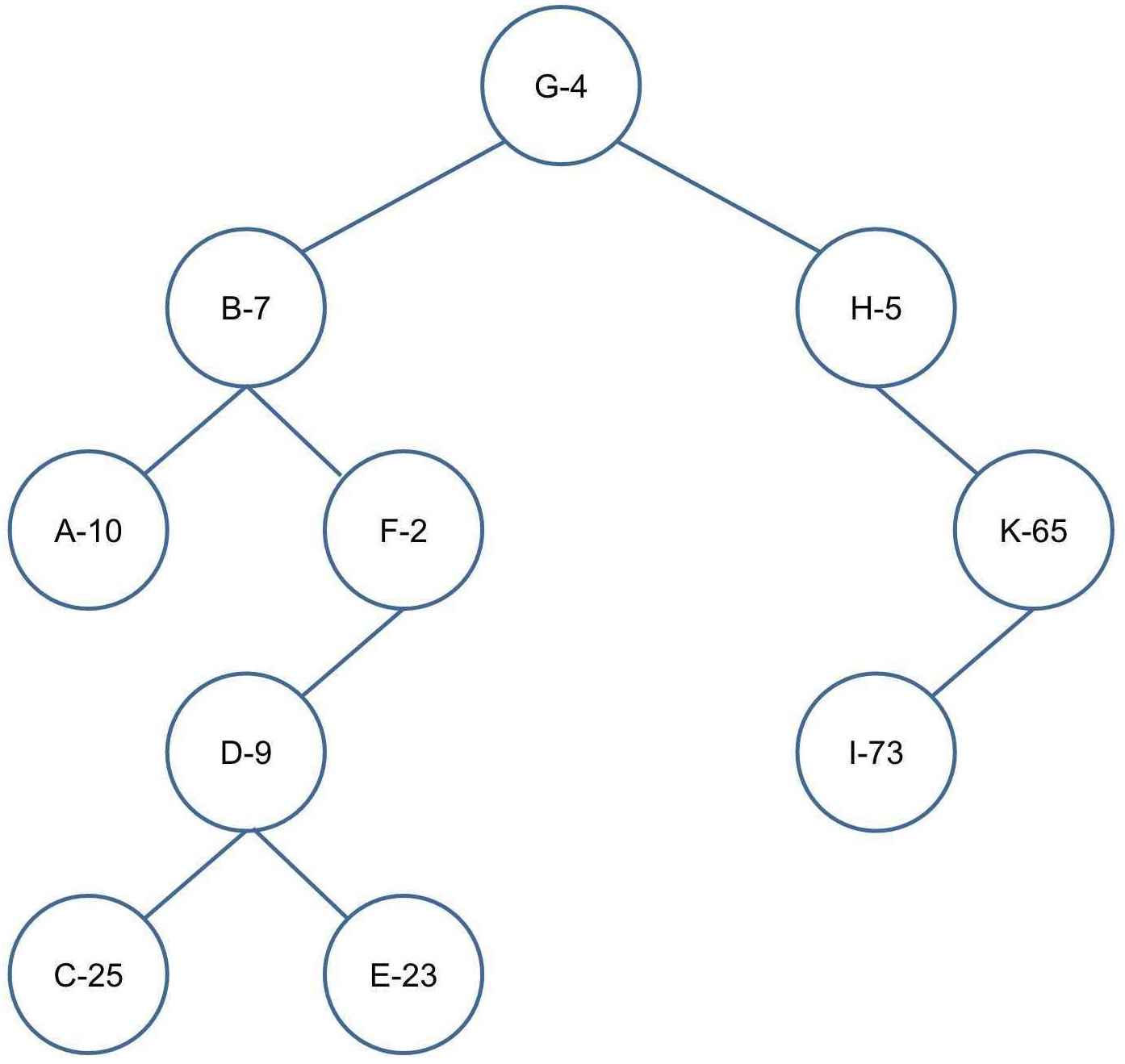
   左旋

   

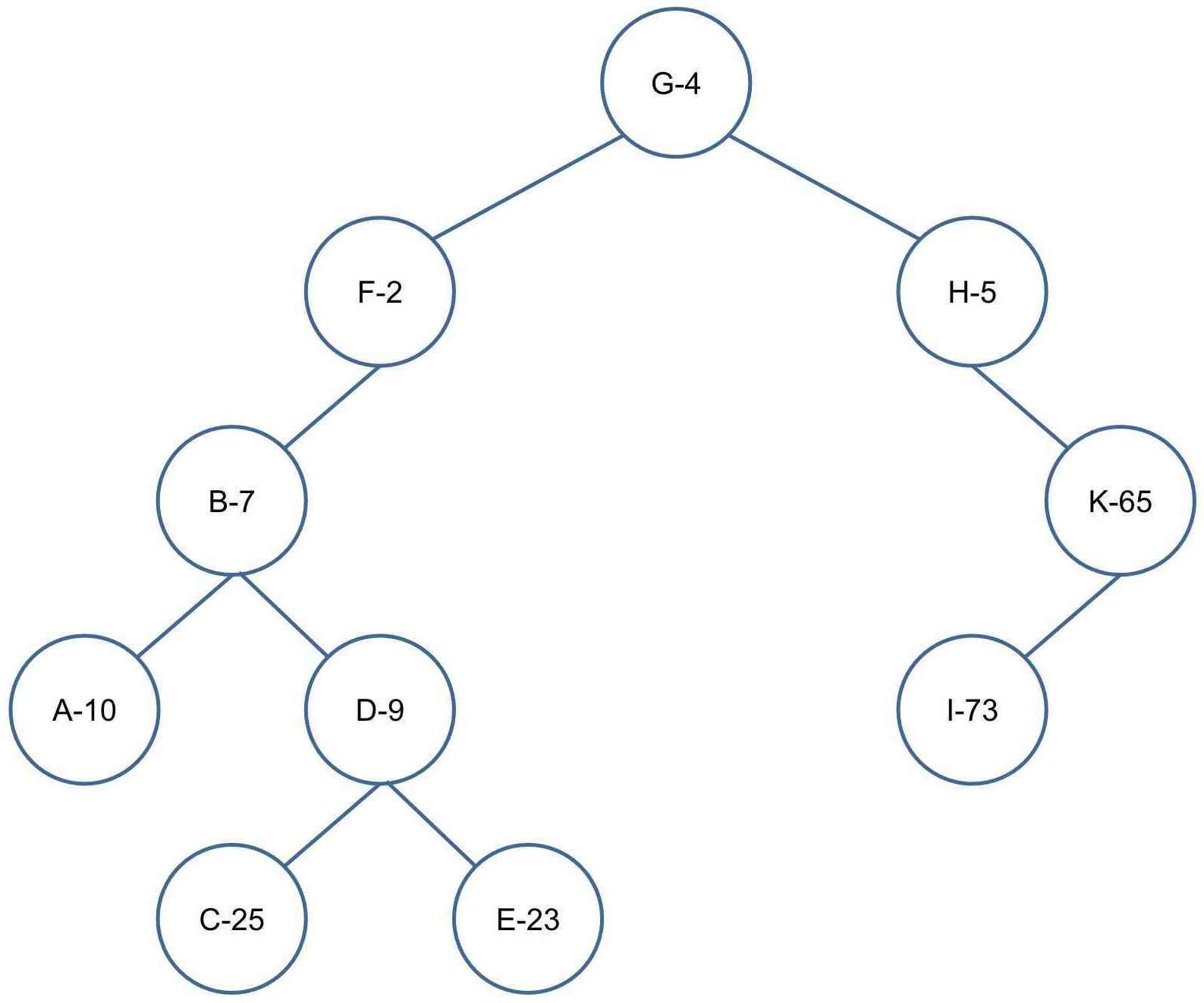
   右旋

   

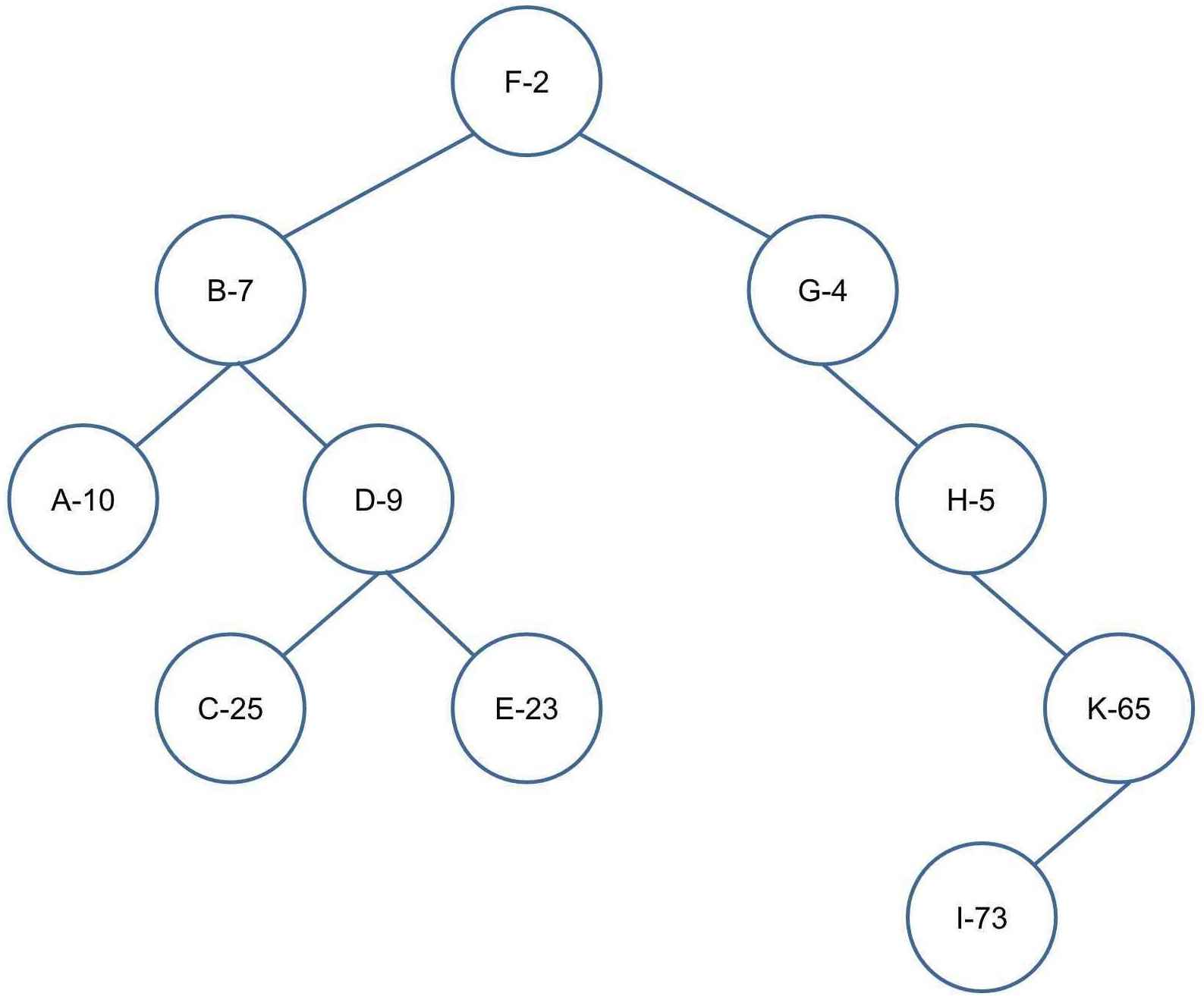
2. 删除一个数\(k\)。

   利用二叉排序树的性质，先寻找对应的节点，从根节点开始：

   (1)\(k<o.key\)，进入该节点左儿子查找；

   (2)\(k>o.key\)，进入该节点右儿子查找。（注意，在寻找节点的递归过程中，就可以维护路径上节点的\(siz\)值，即每个经过的节点\(siz-1\)）

   找到对应节点时，又分两种情况：

   (1)\(o.val>1\)，\(o.val-1\)即可；

   2. 需要删除这个节点，通常采用二叉排序树的删除方法和旋转结合起来，有如下三种情况：

   <1>若该节点为叶节点，直接删除即可；

   <2>若该节点的子节点中有一个为空，则直接删除该节点，用那个非空的子节点代替；

   <3>在其两个子节点中选取优先级较小的节点旋转上来（左儿子——右旋，右儿子——左旋），再向下递归并旋转，直到满足该节点的子节点中至少有一个为空为止。

3. 查询数\(k\)的排名。

   依然利用二叉排序树的性质，排名\(k\)前的点，中序遍历时就先遍历到；

   从根节点开始查找，有如下三种情况：

   (1)\(k<o.key\)，向\(o\)的左儿子查找；

   (2)\(k=o.key\)，返回\(o\)的左子树的大小（左儿子的\(siz+1\)）；

   (3)\(k>o.key\)，给答案加上\(o\)的左子树的大小以及\(o.val\)，再向\(o\)的右儿子查找。

4. 查询排名为\(k\)的数。

   和操作三的思路相似，从根节点开始查找，有如下三种情况：

   (1)\(k<o\)的左子树的大小，向\(o\)的左儿子查找；

   2. 在不满足\(1\)的情况下，若\(k<o\)的左子树的大小\(+o.val\)，即排名为\(k\)的点不在\(o\)的左子树上，也不在\(o\)的右子树上，该节点的关键字就是答案，返回\(o.key\)；

   3. 上述两种情况都不满足，即\(k\)在\(o\)的右子树上，向\(o\)的右儿子查找，但是向下递归传过去的\(k\)要减去\(o\)的左子树的大小和\(o.val\)（左半边的排名已经计算在内，向右子树查找时需要把它排除在外）；

5. 查询数\(k\)的前驱（比\(k\)小的最大的数）。

   首先，这个数一定在\(k\)的左子树上（比\(k\)小），查找到了\(k\)的左子树，就要一直向右子树查找（让这个数尽量大），直到查找到空节点为止，第二个过程中不断更新答案\(ans\)即可；注意\(ans\)初值赋\(-INF\)；

6. 查询数\(k\)的后继（比\(k\)大的最小的数）。

   与操作五相反，这里不再过多赘述；

另外：

1. 有查询操作时，需要注意是否保证有合法结果，没有合法结果要输出什么；

2. NOI 系列比赛中，程序不允许获取当前时间，所以随机数不能撒时间种子，一般以数据范围\(n\)作为种子；

实现

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=,INF=100000000;
int n,cnt,ans,root,ret;
struct treap
{
    int lc,rc,key,pri,siz,val;
}a[MAXN];
void push_up(int o)
{
    a[o].siz=a[a[o].lc].siz+a[a[o].rc].siz+a[o].val;
    return;
}
void lturn(int &o)
{
    int t=a[o].rc;
    a[o].rc=a[t].lc;
    a[t].lc=o;
    a[t].siz=a[o].siz;
    push_up(o);
    o=t;
    return;
}
void rturn(int &o)
{
    int t=a[o].lc;
    a[o].lc=a[t].rc;
    a[t].rc=o;
    a[t].siz=a[o].siz;
    push_up(o);
    o=t;
    return;
}
void insert(int &o,int k)
{
    if(!o)
    {
        o=++cnt;
        a[o]=(treap){0,0,k,rand(),1,1};
        return;
    }
    ++a[o].siz;
    if(k==a[o].key)++a[o].val;
    else if(k<a[o].key)
    {
        insert(a[o].lc,k);
        if(a[o].pri<a[a[o].lc].pri)rturn(o);
    }
    else
    {
        insert(a[o].rc,k);
        if(a[o].pri<a[a[o].rc].pri)lturn(o);
    }
    return;
}
void del(int &o,int k)
{
    if(!o)return;
    if(k==a[o].key)
    {
        if(a[o].val>1)
        {
            --a[o].siz;
            --a[o].val;
        }
        else if(!(a[o].lc*a[o].rc))o=a[o].lc+a[o].rc;
        else if(a[a[o].lc].pri<a[a[o].rc].pri)
        {
            lturn(o);
            del(o,k);
        }
        else
        {
            rturn(o);
            del(o,k);
        }
    }
    else if(k<a[o].key)
    {
        --a[o].siz;
        del(a[o].lc,k);
    }
    else
    {
        --a[o].siz;
        del(a[o].rc,k);
    }
    return;
}
int query_rank(int o,int k)
{
    if(!o)return 0;
    if(k<a[o].key)return query_rank(a[o].lc,k);
    if(k==a[o].key)return a[a[o].lc].siz+1;
    return a[a[o].lc].siz+a[o].val+query_rank(a[o].rc,k);
}
int query_num(int o,int k)
{
    if(!o)return 0;
    if(k<=a[a[o].lc].siz)return query_num(a[o].lc,k);
    if(k<=a[a[o].lc].siz+a[o].val)return a[o].key;
    return query_num(a[o].rc,k-a[a[o].lc].siz-a[o].val);
}
void query_pro(int o,int k)
{
    if(!o)return;
    if(k<=a[o].key)query_pro(a[o].lc,k);
    else
    {
        ret=a[o].key;
        query_pro(a[o].rc,k);
    }
    return;
}
void query_sub(int o,int k)
{
    if(!o)return;
    if(k>=a[o].key)query_sub(a[o].rc,k);
    else
    {
        ret=a[o].key;
        query_sub(a[o].lc,k);
    }
    return;
}
int main()
{
    scanf("%d",&n);
    srand(n);
    int t1,t2;
    for(int i=1;i<=n;++i)
    {
        scanf("%d%d",&t1,&t2);
        if(t1==1)insert(root,t2);
        else if(t1==2)del(root,t2);
        else if(t1==3)printf("%d\n",query_rank(root,t2));
        else if(t1==4)printf("%d\n",query_num(root,t2));
        else if(t1==5)
        {
            ret=-INF;
            query_pro(root,t2);
            printf("%d\n",ret);
        }
        else
        {
            ret=INF;
            query_sub(root,t2);
            printf("%d\n",ret);
        }
    }
    return 0;
}