树状数组

定义

树状数组（Binary Indexed Tree,BIT）是用于解决区间查询，单点修改的一种数据结构。

构造方法

思路

区间求和问题，比较简单的想法就是维护前缀和，可以做到\(O(1)\)的查询速度，但是如果需要给某个数加上一个量\(x\)，只能一个一个修改，复杂度会到\(O(n)\)，这时诞生出一种数据结构-树状数组，来解决这个问题。

顾名思义，树状数组就是用一个数组来实现一个树形结构，而我们还知道一个性质（二进制拆分定理）：任意正整数可以分解为若干个以\(2\)为底数的幂的和，比如\(10\)可以看做\(2^1+2^3\)，\(7\)可以看做\(2^0+2^1+2^2\)，\(14\)可以看做\(2^1+2^2+2^3\)（这个定理的倒过来执行就是把二进制数转化为十进制数的过程），这时可以想到构建将二者结合起来：构建一棵二叉树，每个节点都表示一段区间（的和），而每个节点表示的区间的长度都是\(2\)的整数次幂，而区间长度随着节点深度的增大而减小（求每个节点具体表示的区间长度稍后讨论）。

这样，一段前缀和就可以分解为几段不相交的子区间，具体可以看下图：

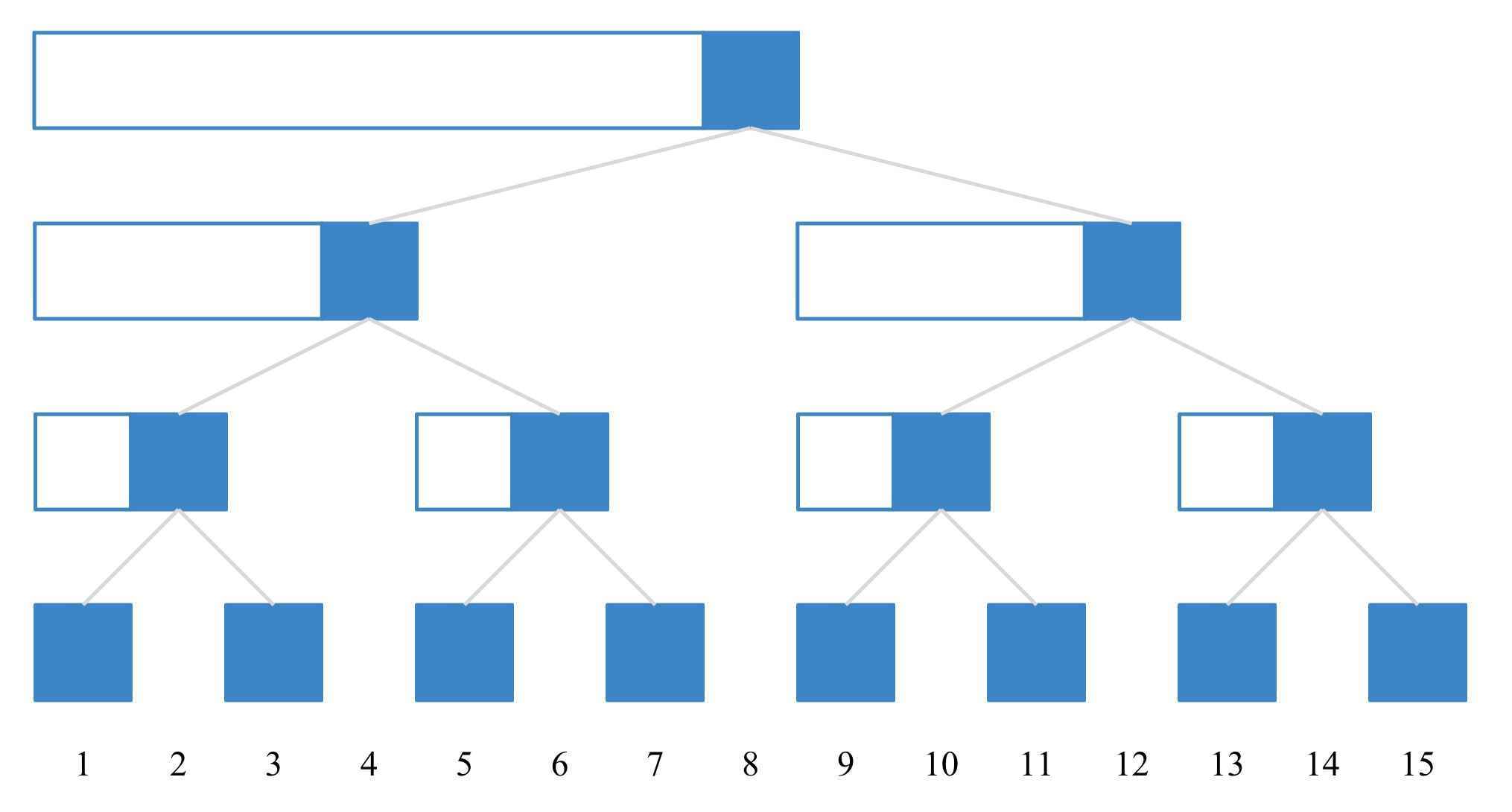
（这棵树中所示的“边”都不存在，也不需要在程序中实现，只是为了演示方便）

其中\(1\sim 7\)、\(1\sim 10\)、\(1\sim 14\)这几段前缀和分别可以分解为：

\(0\)这个节点也并不存在，也不代表任何区间，它是在程序实现时的一个退出标志；

开始牵扯到实现，讨论每个节点表示的区间长度，观察下表：

我们可以发现，节点表示的区间长度，就是该节点编号的二进制最末尾的\(1\)及其后面的\(0\)所表示的数（就是拆分数的时候，几个幂中最小的指数），它有两种求法，都通过位运算实现，通常称之为低位技术（lowbit）（下文直接将节点\(x\)表示的区间长度称为节点\(x\)的 lowbit 值）：

1. \(lowbit(x)=x-(x\ \& \ (x-1))\) \(x-1\)使\(x\)末尾的几个\(0\)变成了\(1\)，最后一个\(1\)变成了\(0\)，其余不变，之后与\(x\)，使得最后一个\(1\)和最后几个\(0\)全部变成了\(0\)，再用\(x\)减这个数，得到答案；

2. \(lowbit(x)=x\ \& \ -x\) 计算机用补码存储有符号整数，一个正数的补码时他本身，一个负数的补码是原数取反\(+1\)得到的； 最终的结果就是，负数的补码相对于其所对应的正数，最后一个\(1\)以及其后面的\(0\)不变，之前的部分全部取反，正负数做与运算得到答案；

显然 ，这种运算方式不仅好写，而且稍快；

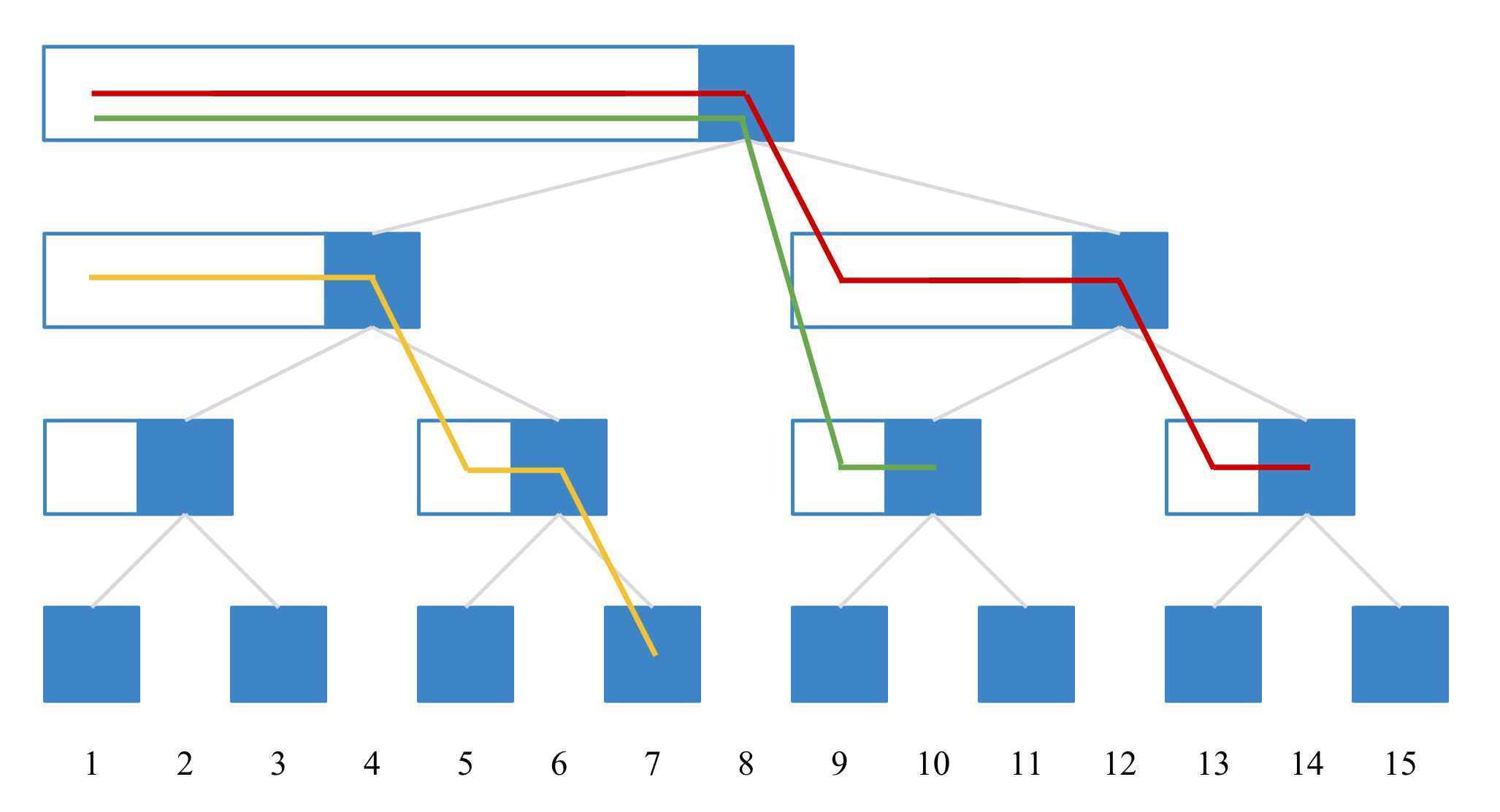
1. 查询前缀和\(1\sim o\)时，从节点\(o\)开始，\(ans\)加上该节点表示的区间和\(sum[o]\)，之后\(o\)减去该节点的 lowbit 值，如此往复直到\(o=0\)为止。

   原理：

   1. 因为前缀和是一段连续的区间，而在这棵树上，以\(x\)为终点的节点有且只有编号为\(x\)的节点，所以结算完节点\(x\)，减去它表示的区间长度，跳到\(y=x-lowbit(x)\)这个节点，它表示区间的终点就是\(x-lowbit(x)\)，紧接在节点\(x\)表示的区间的前面；

   2. 求\(ans\)的过程其实就是指数从小到大来分解这个数的过程。

2. 给编号为\(o\)的数增加\(x\)，从节点\(o\)开始，树状数组\(sum[o]\)加上\(x\)，之后\(o\)加上该节点的 lowbit 值，如此往复直到\(o=n\)为止。

   原理：

   由去掉一个节点编号最末尾那个\(1\)（假设在第\(k\)位），也就是减掉最小的幂之后得到的数，正好是该区间前面的那个节点的编号，于是，给一个数减去其 lowbit 值，再\(+1\)，得到的是该区间的第一个数，由于这是一段连续的区间，所以编号一直\(+1\)，直到需要给第\(k\)位进位的时候停止，这期间加过的就是区间内的数。 即：\(x\)节点表示的区间中包含的数（除了\(x\)本身），其二进制第\(k\)位之前与\(x\)相同，第\(k\)位为\(0\)，第\(k\)位之后至少有一个\(1\)，举个栗子： \(12(1100)\)节点表示的区间包含\(9(1001)\)、\(10(1010)\)、\(11(1011)\)，即\(1100\)中第一个\(1\)不变，第二个\(1\)变成\(0\)，后面两位是\(1\)和\(0\)的组合，且至少有一个\(1\)。 那么反过来想，寻找包含节点\(o\)的深度最深的节点就可以找到其二进制最结尾的数个\(1\)，将其变为\(0\)，再把高一位的\(0\)补成\(1\)； 这个步骤循环进行，就可以修改包含节点\(o\)的所有节点，再举个栗子： 找包含\(43(101011)\)的节点：

   1. 将末尾的两个\(1\)变成\(0\)，再将右起第三位改成\(1\)，变成\(44(101100)\)；

   2. 将末尾的两个\(1\)变成\(0\)，再将左起第五位改成\(1\)，变成\(48(110000)\)；

   3. 将两个\(1\)变成\(0\)，再在高位上补\(1\)，变成\(64(1000000)\)。 如此往复，直至上限。

   我们又发现，去\(1\)再补\(1\)的这个过程，可以直接由原数加上其 lowbit 值来实现，即\(101011+1=101100\)，\(101100+100=110000\)，\(110000+10000=1000000\)……

3. 初始化，维护前缀和数组\(pre\)，\(sum[o]=pre[o]-pre[o-lowbit[o]]\)。

实现

int lowbit(int x)
{
    return x&-x;
}
void change(int o,int x)
{
    while(o<=n)
    {
        c[o]+=x;
        o+=lowbit(o);
    }
    return;
}
int query(int o)
{
    int ans=0;
    while(o>0)
    {
        ans+=c[o];
        o-=lowbit(o);
    }
    return ans;
}