发表更新算法11 分钟读完 (大约1600个字)

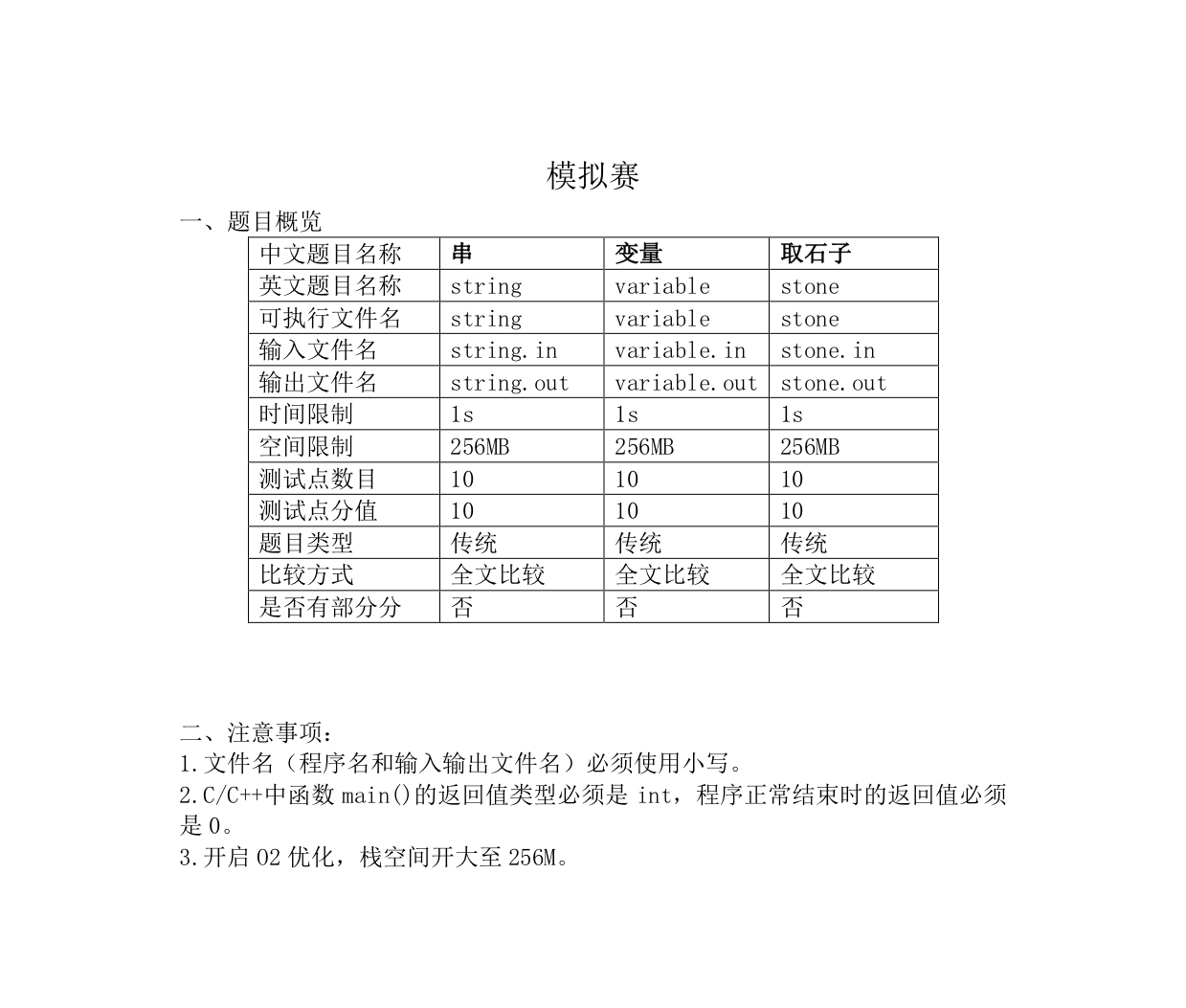
2018-01-02 测试 解题报告

T1

题解

对于 100%的数据： 首先如果\(s\)不是回文串，答案为\(1\)。 否则尝试把\(s\)分成两部分\(s[1\ldots i],s[i+1\ldots n],\quad 1\leq i< n\)，如果存在一种分法使得两个串都不是回文串，答案为\(2\)。 否则每种分法中的两个串都至少有一个是回文串，可以有如下情况：

  1. \(s[1]\not =s[2]\)： 假设\(s[1]=a,s[2]=b\)，这时\(s[n]=s[1]=a,s[n-1]=s[2]=b\)，又\(s[1\ldots 2]\)不是回文串，则\(s[3\ldots n]\)是回文串，即\(s[1\ldots n-2]\)是回文串，即\(s[3]=s[1]=a,s[4]=s[2]=b\)，这时又\(s[1\ldots 4]\)不是回文串，则\(s[5\ldots n]\)是回文串…… 这样循环下去，在\(n\)为奇数时，\(s\)大概是这个形式：\(abababa\)。

  2. \(s[1]=s[2]\)： 假设\(s[1]=s[2]=a\)，这时\(s[n]=s[1]=s[n-1]=s[2]=a\)，无论\(s[1\ldots 2]\)是不是回文串，\(s[n-2]=s[3]=a\)…… 这样循环下去，在\(n\)为奇数时，\(s\)大概是这个形式：\(aaaaaaa\)，或者这个样式：\(aaabaaa\)。在\(n\)为偶数时，\(s\)大概是这个形式：\(aaaaaa\)。

以上几种形式都无解。 于是在\(s\)是回文串时先判断是否满足几种无解情况，否则答案为\(2\)。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<cstdio>
#include<cstring>
#include<algorithm>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long LL;
typedef double db;
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-')f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+ch-'0'; ch=getchar(); }
    return x*f;
}
const int MAXN=1e5+10;
int n;
char a[MAXN];
bool flag,flag1,flag2;
int main()
{
    freopen("string.in","r",stdin);
    freopen("string.out","w",stdout);
    int T=read();
    while(T--)
    {
        n=read();
        scanf("%s",a+1);
        flag=true;
        for(int i=1,j=n;i<=n/2;++i,--j)
            if(a[i]!=a[j])
            {
                flag=false;
                break;
            }
        if(!flag)
        {
            puts("1");
            continue;
        }
        for(int i=2;i<=n/2;++i)
            if(a[i]!=a[i-1])
            {
                flag=false;
                break;
            }
        if(flag)
        {
            puts("-1");
            continue;
        }
        flag1=true;flag2=true;
        for(int i=1;i<=n;i+=2)
            if(a[i]!=a[1])flag1=false;
        for(int i=2;i<=n;i+=2)
            if(a[i]!=a[2])flag2=false;
        if(flag1&&flag2)puts("-1");
        else puts("2");
    }
    return 0;
}

T2

题解

最小割……蛮神奇的。 首先\(W\)或者\(-W\)可以认为是\(1\)或者\(-1\)。 开始时\(w[i]\)的系数为\(1\)。 把\(H_i\)式子中后三项提出来，把\(d-f,e-d,f-e\)加到对应\(w[i]\)的系数上。 绝对值先暂时作为另一个变量，把每一个绝对值项的系数加起来。 从源点向\(w[i]\)连边，容量为负的系数，割这条边表示\(w[i]\)的权值为\(-W\)。 从\(w[i]\)向汇点连边，容量为正的系数，割这条边表示\(w[i]\)的权值为\(W\)。 先看\(q\)个条件：

  1. \(r=0\)时，不能有\(w[x]=W,w[y]=-W\)，于是从\(w[x]\)向\(w[y]\)连边，容量为\(INF\)；
  2. \(r=1\)时，不能有\(w[x]=W,w[y]=-W\)或者\(w[x]=-W,w[y]=W\)，于是从\(w[x]\)向\(w[y]\)连边，容量为\(INF\)，从\(w[y]\)向\(w[x]\)连边，容量为\(INF\)；
  3. \(r=2\)时，只能有\(w[x]=-W,w[y]=W\)，于是从源点向\(w[x]\)连边，容量为\(INF\)，从\(w[y]\)向汇点连边，容量为\(INF\)。

对于一个绝对值项\(a|w[x]-w[y]|\)： 当\(w[x]=W,w[y]=-W\)或者\(w[x]=-W,w[y]=W\)时为\(0\)，否则为\(2aW\)。 故从\(w[x]\)向\(w[y]\)连边，容量为\(2a\)，从\(w[y]\)向\(w[x]\)连边，容量为\(a\)。 答案算出来乘\(W\)即可，负权值需要稍微处理一下。 （这道题可以不拆点，我推导这个图的时候觉得拆开来画着好看，于是代码里也拆了……）

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
typedef long long LL;
typedef double db;
inline LL read()
{
    LL x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-')f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+ch-'0'; ch=getchar(); }
    return x*f;
}
const int MAXN=510;
const LL INF=1e15,HALF=1e9;
int n,p,q,head[MAXN*2],cnt,idx[MAXN*2],S,T;
LL w,val1[MAXN],val2[MAXN][MAXN];
struct edge
{
    int v,next;
    LL val;
}e[MAXN*200];
void addedge(int x,int y,LL z)
{
    e[cnt]=(edge){y,head[x],z};
    head[x]=cnt++;
    swap(x,y);
    e[cnt]=(edge){y,head[x],0};
    head[x]=cnt++;
    return;
}
void bfs()
{
    memset(idx,0,sizeof(idx));
    idx[S]=1;
    queue<int>q;
    q.push(S);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];~i;i=e[i].next)
        {
            int v=e[i].v;
            if(idx[v]||!e[i].val)continue;
            idx[v]=idx[u]+1;
            q.push(v);
        }
    }
    return;
}
LL dfs(int u,LL _min)
{
    if(u==T)return _min;
    LL ret=0,k;
    for(int i=head[u];~i;i=e[i].next)
    {
        int v=e[i].v;
        if(idx[v]!=idx[u]+1||!e[i].val)continue;
        k=dfs(v,min(_min-ret,e[i].val));
        e[i].val-=k;
        e[i^1].val+=k;
        ret+=k;
        if(ret==_min)break;
    }
    return ret;
}
LL dinic()
{
    LL ret=0;
    while(true)
    {
        bfs();
        if(!idx[T])break;
        ret+=dfs(S,INF);
    }
    return ret;
}
int main()
{
    freopen("variable.in","r",stdin);
    freopen("variable.out","w",stdout);
    int Ta=read();
    while(Ta--)
    {
        n=read();w=read();p=read();q=read();
        memset(head,-1,sizeof(head));
        memset(val1,0,sizeof(val1));
        memset(val2,0,sizeof(val2));
        cnt=0;
        for(int i=1;i<=n;++i)val1[i]=1;
        for(int i=1;i<=p;++i)
        {
            LL x=read(),y=read(),z=read(),a=read(),b=read(),c=read(),d=read(),e=read(),f=read();
            val1[x]+=d-f;val1[y]+=e-d;val1[z]+=f-e;
            val2[x][y]+=a;val2[y][x]+=a;
            val2[y][z]+=b;val2[z][y]+=b;
            val2[x][z]+=c;val2[z][x]+=c;
        }
        S=0;T=2*n+1;
        for(int i=1;i<=q;++i)
        {
            int x=read(),y=read(),r=read();
            if(!r)
                addedge((x<<1)-1,y<<1,INF);
            if(r==1)
            {
                addedge((x<<1)-1,y<<1,INF);
                addedge((y<<1)-1,x<<1,INF);
            }
            if(r==2)
            {
                addedge(S,(y<<1)-1,INF);
                addedge(x<<1,T,INF);
            }
        }
        for(int i=1;i<=n;++i)
        {
            addedge(S,(i<<1)-1,HALF-val1[i]);
            addedge((i<<1)-1,i<<1,INF);
            addedge(i<<1,T,HALF+val1[i]);
            for(int j=i+1;j<=n;++j)
            {
                if(!val2[i][j])continue;
                addedge((i<<1)-1,j<<1,val2[i][j]<<1);
                addedge((j<<1)-1,i<<1,val2[i][j]<<1);
            }
        }
        printf("%lld\n",(dinic()-HALF*n)*w);
    }
    return 0;
}

T3

题解

先默认\(a<b\)。 对于每一堆石子\(x\)先对\(a+b\)取模，然后分成四种情况：

  1. \(x < a\)，没用；
  2. \(a\leq x < b\)，只要存在 A 必胜；
  3. \(b\leq x < 2a\)，这种无论谁拿一次都会变成情况 1，和 4 一起讨论。
  4. \(2a\leq x\)，这种 A 拿一次就变成 2，B 拿一次就变成 1。

如果 4 存在至少\(2\)个就 A 必胜； 存在\(1\)个，若 3 是偶数则先手必胜，否则 A 必胜； 不存在，若 3 是偶数则后手必胜，否则先手必胜。 统计情况时，存在至少两个是\(2^x-x-1\)，存在一个是\(x\)，奇数个和偶数个都是\(2^{x-1}\)。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<cstdio>
#include<cstring>
#include<algorithm>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long LL;
typedef double db;
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-')f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+ch-'0'; ch=getchar(); }
    return x*f;
}
const LL MOD=1e9+7;
int n,a,b;
LL x[4],f[4];
bool flag;
LL qpow(LL a,LL b)
{
    LL ret=1;
    for(;b;b>>=1,a=a*a%MOD)
        if(b&1)ret=ret*a%MOD;
    return ret;
}
LL odd_even(LL x,bool k)
{
    return x?qpow(2,x-1):k;
}
int main()
{
    freopen("stone.in","r",stdin);
    freopen("stone.out","w",stdout);
    n=read();a=read();b=read();
    if(a>b)swap(a,b),flag=true;
    for(int i=1;i<=n;++i)
    {
        int t=read()%(a+b);
        if(t<a)++x[0];
        else if(t<b)++x[1];
        else if(t<2*a)++x[2];
        else ++x[3];
    }
    f[0]=(((qpow(2,x[1])-1)*qpow(2,x[2]+x[3])%MOD+(qpow(2,x[3])-x[3]-1+MOD)%MOD*qpow(2,x[2])%MOD)%MOD+x[3]*odd_even(x[2],0)%MOD)%MOD;
    f[2]=(x[3]*odd_even(x[2],1)%MOD+odd_even(x[2],0))%MOD;
    f[3]=odd_even(x[2],1);
    for(int i=0;i<4;++i)
        f[i]=f[i]*qpow(2,x[0])%MOD;
    if(flag)swap(f[0],f[1]);
    for(int i=0;i<4;++i)
        printf("%lld ",f[i]);
    puts("");
    return 0;
}

2018-01-02 测试 解题报告

https://blog.xqmmcqs.com/2018-01-02测试 解题报告/

作者

xqmmcqs

发布于

2018-01-03

更新于

2023-03-29

许可协议

#

评论

目录

最新文章

分类

Your browser is out-of-date!

Update your browser to view this website correctly.&npsb;Update my browser now

×

×