发表更新算法20 分钟读完 (大约2969个字)

二分图相关

定义

二分图又称作二部图，是图论中的一种特殊模型。 设\(G=(V,E)\)是一个无向图，如果顶点\(V\)可分割为两个互不相交的子集\((U,V)\)，并且图中的每条边\((i,j)\)所关联的两个顶点\(i\)和\(j\)分别属于这两个不同的顶点集，则称图\(G\)为一个二分图。

一个无向图为二分图的充要条件是没有奇环。

二分图染色

求解算法

思路

判定一个图是否为二分图，使用 dfs 进行黑白染色，判定能否满足每条边的两个顶点异色。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=,MAXM=;
int n,m,cnt,col[MAXN],head[MAXN],ans;
struct edge
{
    int v,next;
}e[MAXM*2];
void addedge(int x,int y)
{
    e[++cnt]=(edge){y,head[x]};
    head[x]=cnt;
    return;
}
bool dfs(int u,int x)
{
    if(col[u])
    {
        if(col[u]==x)return true;
        return false;
    }
    col[u]=x;
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].v;
        if(!dfs(v,x==1?2:1))return false;
    }
    return true;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        addedge(x,y);
        addedge(y,x);
    }
    bool flag=true;
    for(int i=1;i<=n;++i)
        if(!col[i])
            if(!dfs(i,1))
            {
                flag=false;
                break;
            }
    flag?puts("Yes"):puts("No");
    return 0;
}

二分图最大匹配

定义

又称最大边独立集，即边数最多的匹配。

有关概念

匹配：又称边独立集，一个边集，满足边集中的任两边不邻接。

极大匹配：又称极大边独立集，本身是匹配，加入任何边就不是。

增广路：连接两个未匹配结点的路径，且已匹配边和未匹配边在路径上交替出现，可以发现非匹配边的数量比匹配边的数量多\(1\)，故将路径上的每一条边取反就能使匹配边的数量\(+1\)。

求解算法

匈牙利算法

思路

  1. 在图中找出增广路；
  2. 对增广路上每一条边取反（即匹配边改为非匹配边，非匹配边改为匹配边）；
  3. 重复以上两步直到找不到增广路为止。

样例推导

给出二分图：

从\(X1\)开始，找到增广路\(X1-Y1\)，标记\(X1-Y1\)为匹配边；

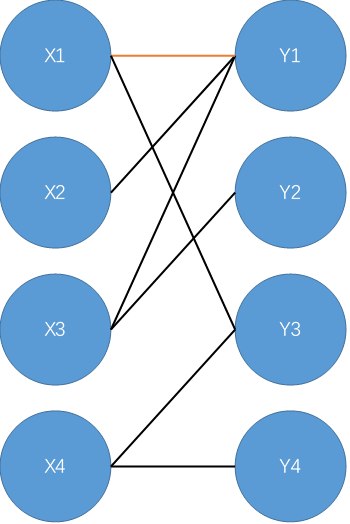
从\(X2\)开始，找到增广路\(X2-Y1-X1-Y3\)；

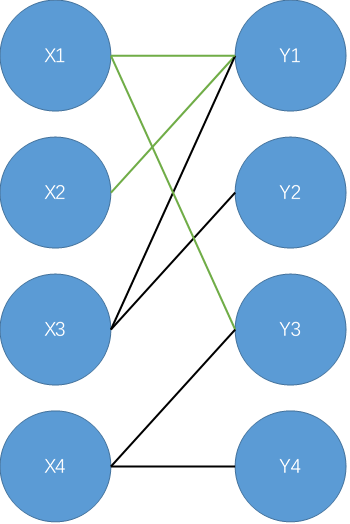
标记\(X1-Y1\)为非匹配边，标记\(X1-Y3,X2-Y1\)为匹配边；

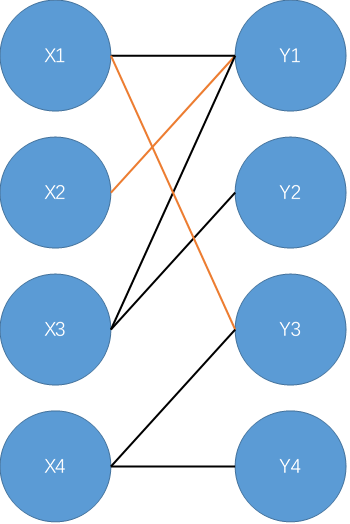
从\(X3\)开始，找到\(X3-Y1-X2\)，不是增广路；

找到增广路\(X3-Y2\)，标记\(X3-Y2\)为匹配边；

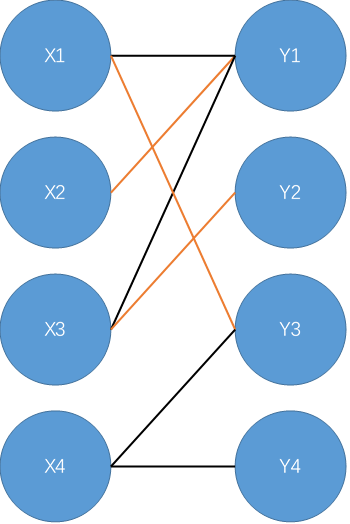
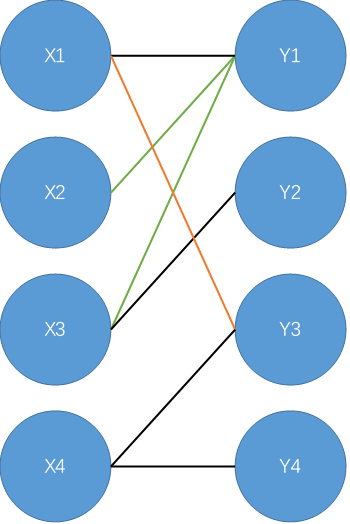
从\(X4\)开始，找到\(X4-Y3-X1-Y1-X2\)，不是增广路；

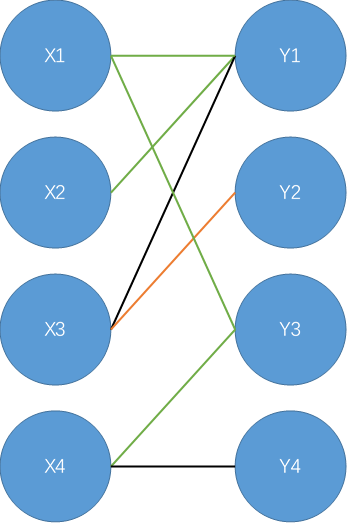
找到增广路\(X4-Y4\)，标记\(X4-Y4\)为匹配边。

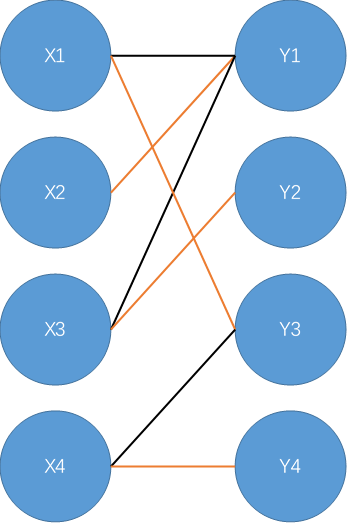
至此找出最大匹配。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=,MAXM=;
int n,m,cnt,match[MAXN],head[MAXN],ans;
bool vis[MAXN];
struct edge
{
    int v,next;
}e[MAXM*2];
void addedge(int x,int y)
{
    e[++cnt]=(edge){y,head[x]};
    head[x]=cnt;
    return;
}
bool Hungary(int u)
{
    for(int i=head[u];i;i=e[i].next)
    {
        int v=e[i].v;
        if(!vis[v])
        {
            vis[v]=true;
            if(!match[v]||Hungary(match[v]))
            {
                match[v]=u;
                return true;
            }
        }
    }
    return false;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        addedge(x,y);
    }
    for(int i=1;i<=n;i++)
    {
        memset(vis,false,sizeof(vis));
        if(Hungary(i))ans++;
    }
    printf("%d\n",ans);
    return 0;
}

网络流解法

思路

建立源点，向\(Xi\)连边，容量为\(1\)；

若二分图中有边\(i,j\)，则从\(Xi\)向\(Yj\)连边，容量为\(1\)；

建立汇点，\(Yi\)向汇点连边，容量为\(1\)。

使用最大流算法解决。

二分图最小点覆盖

定义

点数最少的点覆盖。

有关概念

点覆盖：一个点集，满足所有边至少有一个端点在集合里。

极小点覆盖：本身是点覆盖，其所有真子集都不是。

求解算法

König 定理：最小点覆盖大小=最大匹配数。

首先，二分图最大匹配满足图中没有增广路；

假设最大匹配数为\(n\)，则\(X\)部和\(Y\)部都各有\(n\)个匹配点，覆盖了\(n\)个匹配边；

对于非匹配边，若它的两个端点都是非匹配点，那么这条非匹配边成一个增广路，和二分图最大匹配的性质不符，故非匹配边的两个顶点一定是一个匹配点和一个非匹配点，或者两个匹配点，于是这个非匹配边一定会被匹配点覆盖；

故\(X\)部的\(n\)个匹配点或\(Y\)部的\(n\)个匹配点都可以覆盖所有边，故最小点覆盖大小为\(n\)。

二分图最大独立集

定义

点数最多的独立集。

有关概念

独立集：一个点集，集合中任意两个点不相邻。

极大独立集：本身是独立集，再加入任何点就不是。

求解算法

最大独立集大小=总点数-最大匹配数。

可以用上面的结论：非匹配边的两个顶点一定不会都是未匹配点，故不存在两个非匹配点之间有边，故非匹配点构成独立集；

又有不存在增广路能使最大匹配数变大而使这个独立集变小，故这个独立集是最大独立集。

二分图最大团

定义

点数最多的团。

有关概念

团：一个点集，集合中任意两个点都相邻，对于二分图来说，我们默认\(X\)部的每个点之间和\(Y\)部的每个点之间都有边，故二分图的团是在\(X\)部找一个点集\(S_x\)，在\(Y\)部找一个点集\(S_y\)，使得\(S_x\)中的每一个结点和\(S_y\)中的每个结点之间都有边。

补图：包含原图的所有结点，原图中若两个结点\(Xi,Yj\)之间有边，则补图中没有，否则补图中有。

极大团：本身为团，再加入任何点都不是。

求解算法

最大团=补图的最大独立集。

补图中不相邻的两个结点在原图中一定相邻。

二分图最小边覆盖

定义

边数的最小边覆盖。

有关概念

边覆盖：一个边集，使得所有点都与集合中的边邻接。

极小边覆盖：本身是边覆盖，其所有真子集都不是。

求解算法

最小边覆盖大小=总点数-最大匹配数。

首先设最大匹配数为\(n\)，总点数为\(m\)，每个匹配边可以不重复地覆盖\(2\)个点，故覆盖了\(2n\)个点；

剩下的每条边最多只能覆盖\(1\)个点，故剩下\(m-2n\)个点需要\(m-2n\)条边来覆盖，故最小边覆盖大小为\(m-2n+n=m-n\)。

DAG 最小路径覆盖

定义

用尽量少的不相交简单路径覆盖 DAG 的所有顶点。

有关概念

DAG：有向无环图。

链：一个点集，其中任意两点\(u\)、\(v\)可以到达，要么\(u\)能走到\(v\)，要么\(v\)能走到\(u\)。

反链：一个点集，其中任意两点均不可到达。

最大（长）反链：反链中点数最多的一个（=最小路径覆盖数）。

求解算法

思路

由最小路径覆盖数=DAG 的点数-最小路径覆盖的边数。

把原图的所有节点拆成\(Xi\)和\(Yi\)，如果 DAG 中存在边\(i,j\)就在二分图中连有向边\(Xi,Yj\)，跑二分图匹配。

容易得出最大匹配数就是最小路径覆盖的边数，故最小路径覆盖数=DAG 的点数-最大匹配数。

二分图最大权匹配

定义

若二分图的每条边都有一个权值\(v[i][j]\)，求一种完美匹配，使得所有匹配边的权值和最大，记做最优完美匹配。

有关概念

完美匹配：又称完备匹配，匹配了所有点的匹配。

可行顶标：对于二分图的每个点给定一个顶标值，用\(lx[i]\)​记录\(X\)​部的顶标，用\(ly[i]\)​记录\(Y\)​部的顶标。对于图中任意一条边\((Xi,Yj)\)​满足\(lx[i]+ly[j]\geq v[i][j]\)​。

相等子图：原图的一个生成子图，包含原图的所有点，但是只包含\(lx[i]+ly[j]=v[i][j]\)的边（可行边）。

求解算法

KM 算法

思路

定理：如果原图的一个相等子图中包含完美匹配，那么这个匹配就是原图的最佳完美匹配。

初始化\(lx[i]=max{v[i][j]},\quad 1\leq j\leq n\)​​，\(ly[i]=0\)​​，此时满足\(lx[i]+ly[j]\geq v[i][j]\)​​。

我们通过修改顶标的方式扩大相等子图，寻找完美匹配。

从\(X\)部的每一个点开始增广，保证增广路径上都是可行边：

若能找到一条增广路，这个点完成配对；

否则在当前增广路径上的所有\(X\)部结点顶标减去\(a\)，所有\(Y\)部顶标加上\(a\)。

此时有如下四种情况：

  1. \(Xi\)和\(Yj\)都属于增广路径，\(lx[i]+a+ly[j]-a\)不变，故\((i,j)\)仍然为可行边。
  2. \(Xi\)和\(Yj\)都不属于增广路径，\(lx[i]+ly[j]\)不变，故\((i,j)\)可行性不变。
  3. \(Xi\)不属于增广路径，\(Yj\)属于增广路径，\(lx[i]+ly[j]+a\)增大，\((i,j)\)仍然不可能加入相等子图。
  4. \(Xi\)属于增广路径，\(Yj\)不属于增广路径，\(lx[i]-a+ly[j]\)减小，\((i,j)\)有可能会加入相等子图。

所以进行修改操作后，原来的可行边仍然可行，不可行边有可能加入相等子图。

上述四种情况只有第四种可行性可能发生改变，故取所有第四种情况的边，\(a=\min\{lx[i]+ly[i]-v[i][j]\}\)​。

这样就能保证每次都有至少一个边加入相等子图。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=,INF=0x3f3f3f3f;
int n,e[MAXN][MAXN],match[MAXN],lx[MAXN],ly[MAXN],slack[MAXN];
bool visx[MAXN],visy[MAXN];
bool dfs(int x)
{
    visx[x]=true;
    for(int y=1;y<=n;++y)
    {
        if(visy[y])continue;
        int t=lx[x]+ly[y]-e[x][y];
        if(!t)
        {
            visy[y]=true;
            if(!match[y]||dfs(match[y]))
            {
                match[y]=x;
                return true;
            }
        }
        else slack[y]=min(slack[y],t);
    }
    return false;
}
int KM()
{
    memset(match,0,sizeof(match));
    memset(ly,0,sizeof(ly));
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j)
            lx[i]=max(lx[i],e[i][j]);
    for(int i=1;i<=n;++i)
    {
        memset(slack,0x3f3f3f3f,sizeof(slack));
        while(true)
        {
            memset(visx,0,sizeof(visx));
            memset(visy,0,sizeof(visy));
            if(dfs(i))break;
            int d=INF;
            for(int j=1;j<=n;++j)if(!visy[j])d=min(d,slack[j]);
            for(int j=1;j<=n;++j)
            {
                if(visx[j])lx[j]-=d;
                if(visy[j])ly[j]+=d;
                else slack[j]-=d;
            }
        }
    }
    int ret=0;
    for(int i=1;i<=n;++i)ret+=e[match[i]][i];
    return ret;
}
int main()
{
    while(scanf("%d",&n)==1)
    {
        for(int i=1;i<=n;++i)
            for(int j=1;j<=n;++j)
                scanf("%d",&e[i][j]);
        printf("%d\n",KM());
    }
    return 0;
}

网络流解法

思路

建立源点，向\(Xi\)连边，容量为\(1\)，费用为\(0\)；

若二分图中有边\(i,j\)，则从\(Xi\)向\(Yj\)连边，容量为\(INF\)，费用为权值的相反数（由于费用流求出的是最小费用）；

建立汇点，\(Yi\)向汇点连边，容量为\(1\)，费用为\(0\)。

使用费用流算法解决。

二分图相关

https://blog.xqmmcqs.com/二分图相关/

作者

xqmmcqs

发布于

2017-11-27

更新于

2023-03-29

许可协议

#

评论

最新文章

分类

Your browser is out-of-date!

Update your browser to view this website correctly.&npsb;Update my browser now

×

×