概率论与数理统计公式
BUPT 概率论与数理统计课程(计算机学院,4 学分)涉及的公式,自制
简单的就略过了,写在这的不一定都要背。
\[ \begin{align*}\Gamma(\alpha)=\int_0^\infty x^{\alpha-1}e^{-x}\mathop{}\!\mathrm{d}x,\quad\Gamma(\alpha+1)=\alpha\Gamma(\alpha) \\ \Gamma(1)=1,\quad\Gamma(\frac12)=\sqrt\pi,\quad\Gamma(n+1)=n!\ (n\in \mathbf Z^+)\end{align*} \]
第一章
\[ P(A\cup B)=P(A)+P(B)-P(AB) \]
\[ P(A-B)=P(A\overline B)=P(A)-P(AB) \]
\[ P(AB)=P(B|A)P(A) \]
\[ P(A_1A_2\dots A_n)=P(A_n|A_1A_2\dots A_{n-1})P(A_{n-1}|A_1A_2\dots A_{n-2})\dots P(A_2|A_1)P(A_1) \]
\[ P(A)=\sum_{i=1}^nP(B_i)P(A|B_i) \]
\[ P(B_k|A)=\frac{P(B_k)P(A|B_k)}{P(A)}=\frac{P(B_k)P(A|B_k)}{\sum_{i=1}^nP(B_i)P(A|B_i)} \]
第二章
\[ P\{a< X\leq b\}=F(b)-F(a) \]
\[ P\{X<a\}=F(a^-) \]
\[ P\{X=a\}=F(a)-F(a^-) \]
\[ P\{a\leq X <b\}=F(b^-)-F(a^-) \]
\[ P\{a<X<b\}=F(b^-)-F(a) \]
\[ P\{X>a\}=1-P\{X\leq a\}=1-F(a) \]
0-1 分布 \[ P\{X=k\}=p^k(1-p)^{1-k} \] 二项分布\(X\sim B(n,p)\) \[ P\{X=k\}=C_n^kp^k(1-p)^{n-k} \] 泊松分布\(X\sim \pi(\lambda)\) \[ P\{X=k\}=\frac{\lambda^k}{k!}e^{-\lambda} \] 泊松定理 \[ np=\lambda\quad\lim_{n\to \infty}C_n^kp^k(1-p)^{n-k}=\frac{\lambda^ke^{-\lambda}}{k!} \] 均匀分布\(X\sim U(a,b)\) \[ f(x)=\left\{\begin{align*}& \frac 1{b-a}, & a<x<b \\& 0, & else\end{align*}\right. \]
\[ F(x)=\left\{\begin{align*}& 0, & x<a \\& \frac {x-a}{b-a}, & a\leq x<b \\& 1, & x\geq b\end{align*}\right. \]
指数分布\(X\sim E(\lambda)\) \[ f(x)=\left\{\begin{align*}&\lambda e^{-\lambda x}, & x>0 \\& 0, & x\leq 0\end{align*}\right. \]
\[ F(x)=\left\{\begin{align*}&1-e^{-\lambda x}, & x>0 \\ &0, & x\leq 0\end{align*}\right. \]
正态分布\(X\sim N(\mu,\sigma^2)\) \[ f(x)=\frac 1{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \] \(y=\varphi(x)\)严格单调且其反函数 为\(x=h(y)\),则\(Y=\varphi(x)\)的密度为 \[ f_Y(y)=\left\{\begin{align*}&f_X[h(y)]|h'(y)|, & \alpha<y<\beta \\& 0, & else\end{align*}\right. \]
第三章
二维连续型随机变量边缘分布 \[ f_X(x)=\int_{-\infty}^{+\infty}f(x,y)\mathop{}\!\mathrm{d}y\quad f_Y(y)=\int_{-\infty}^{+\infty}f(x,y)\mathop{}\!\mathrm{d}x \] 条件概率密度 \[ f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y{(y)}}\quad f_{Y|X}(y|x)=\frac{f(x,y)}{f_X{(x)}} \] 二维正态分布\((X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)\) \[ f(x,y)=\frac 1{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}e^{-\frac1{2(1-\rho^2)}[\frac{(x-\mu_1^2)}{\sigma_1^2}-2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\frac{(y-\mu_2)^2}{\sigma_2^2}]} \] \(U=X+Y\)的分布 \[ f_U(u)=\int_{-\infty}^{+\infty}f(x,u-x)\mathop{}\!\mathrm{d}x=\int_{-\infty}^{+\infty}f(u-y,y)\mathop{}\!\mathrm{d}y \] 最大值和最小值的分布 \[ F_{\max}(z)=[F(z)]^n\quad F_{\min}(z)=1-[1-F(z)]^n \] \(U=\frac YX\)和\(V=XY\)的分布 \[ f_U(u)=\int_{-\infty}^{+\infty}|x|f(x,xu)\mathop{}\!\mathrm{d}x\quad f_V(v)=\int_{-\infty}^{+\infty}\frac 1{|x|}f\left(x,\frac vx\right)\mathop{}\!\mathrm{d}x \]
第四章
数学期望 \[ E(X)=\sum_k x_kp_k,\quad E(X)=\int_{-\infty}^{\infty}xf(x)\mathop{}\!\mathrm{d}x \] 若\(Y=g(X)\) \[ E(Y)=\int_k g(x_k)p_k,\quad \int_{-\infty}^{\infty}g(x)f(x)\mathop{}\!\mathrm{d}x \] 若\(Z=g(X,Y)\) \[ E(Z)=\sum_{i}\sum_jp_{ij},\quad E(Z)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(x,y)f(x,y)\mathop{}\!\mathrm{d}x\mathop{}\!\mathrm{d}y \] 数学期望的性质 \[ E(C)=C \]
\[ E(aX+bY)=aE(x)+bE(Y) \]
若\(X,Y\)独立 \[ E(XY)=E(X)E(Y) \] 方差 \[ D(X)=E\{[X-E(X)]^2\}=E(X^2)-[E(X)]^2 \] 方差的性质 \[ D(C)=0 \]
\[ D(aX+b)=a^2D(X) \]
\[ D(X\pm Y)=D(X)+D(Y)\pm 2Cov(X,Y) \]
若\(X,Y\)独立 \[ D(X\pm Y)=D(X)+D(Y) \] 常见分布的数学期望和方差
| 分布 | 数学期望 | 方差 |
|---|---|---|
| 0-1 分布 | \(E(X)=p\) | \(D(X)=p-p^2\) |
| \(X\sim B(n,p)\) | \(E(X)=np\) | \(D(X)=np(1-p)\) |
| \(X\sim\pi(\lambda)\) | \(E(X)=\lambda\) | \(D(X)=\lambda\) |
| \(X\sim U(a,b)\) | \(E(X)=\frac{a+b}2\) | \(D(X)=\frac{(b-a)^2}{12}\) |
| \(X\sim E(\lambda)\) | \(E(X)=\frac1\lambda\) | \(D(X)=\frac1{\lambda^2}\) |
| \(X\sim N(\mu,\sigma^2)\) | \(E(X)=\mu\) | \(D(X)=\sigma^2\) |
协方差 \[ Cov(X,Y)=E\{[X-E(X)][Y-E(Y)]\}=E(XY)-E(X)E(Y) \] 协方差的性质 \[ Cov(X,Y)=Cov(Y,X),\quad Cov(X,X)=D(X) \]
\[ Cov(aX,bY)=abCov(X,Y) \]
\[ Cov(aX+bY,Z)=aCov(X,Z)+bCov(Y,Z) \]
相关系数 \[ \rho_{XY}=\frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}} \] 相关系数的性质 \[ \rho_{XY}\leq 1 \] \(|\rho_{XY}|=1\)的充要条件是 \[ P\{Y=aX+b\}=1 \]
第五章
切比雪夫不等式 \[ P\{|X-E(X)|\geq\varepsilon\}\leq\frac{D(X)}{\varepsilon^2} \] 辛钦大数定理
\(X_1,X_2,\dots,X_n,\dots\)独立同分布,\(E(X_k)=\mu\),对于任意给定的\(\varepsilon>0\),有 \[ \lim_{n\to\infty}P\left\{\left|\frac1n\sum_{i=1}^nX_i-\mu\right|<\varepsilon\right\}=1 \] \(\overline X\)依概率收敛于\(\mu\)
中心极限定理
\(X_1,X_2,\dots,X_n,\dots\)独立同分布,\(E(X_k)=\mu,D(X_k)=\sigma^2\) \[ \lim_{n\to\infty}P\left\{\frac{\sum_{i=1}^nX_i-n\mu}{\sqrt n\sigma}\leq x\right\}=\Phi(x) \] \(\eta_n\sim B(n,p)\) \[ \lim_{n\to\infty}P\left\{\frac{\eta_n-np}{\sqrt {np(1-p)}}\leq x\right\}=\Phi(x) \]
第六章
称不含未知参数的样本函数\(g(X_1,X_2,\dots.X_n)\)为统计量 \[ \overline X=\frac 1n\sum_{i=1}^n X_i \] 为样本均值 \[ S^2=\frac 1{n-1}\sum_{i=1}^n(X_i-\overline X)^2 \] 为样本方差 \[ S=\sqrt{S^2} \] 为样本标准差 \[ A_k=\frac 1n\sum_{i=1}^n X_i^k \] 为\(k\)阶样本原点矩 \[ B_k=\frac 1n\sum_{i=1}^n(X_i-\overline X)^k \] 为\(k\)阶样本中心矩
将一个容量为\(n\)的样本值排序并且重新编号,设为 \[ x_{(1)}\leq x_{(2)}\leq \dots\leq x_{(n)} \] 则经验函数\(F_n(x)\)的观察值为 \[ F_n(x)=\left\{\begin{align*}& 0, & x<x_{(1)} \\ & \frac kn, & x_{(k)}\leq x<x_{(k+1)} \\& 1, & x\geq x_{(n)}\end{align*}\right. \]
设\(X_1,X_2,\dots,X_n\)相互独立,都服从\(N(0,1)\),则称随机变量 \[ \chi^2=X_1^2+X_2^2+\dots+X_n^2 \] 所服从的分布为自由度为\(n\)的\(\chi^2\)分布,记为\(\chi^2\sim \chi^2(n)\)
设\(X_i\sim N(\mu,\sigma^2)\),则 \[ \chi^2=\frac1{\sigma^2}\sum_{i=1}^n(X_i-\mu)^2\sim\chi^2(n) \] 设\(X_1\sim \chi^2(n_1),X_2\sim\chi^2(n_2)\),且\(X_1,X_2\)相互独立,则 \[ X_1+X_2\sim\chi^2(n_1+n_2) \]
\[ E(\chi^2)=n,\quad D(\chi^2)=2n \]
设\(X\sim N(0,1),Y\sim \chi^2(n)\),且\(X,Y\)独立,则称随机变量 \[ t=\frac X{\sqrt{Y/n}} \] 服从自由度为\(n\)的\(t\)分布,记为\(t\sim t(n)\) \[ E(t)=0,\quad D(t)=\frac n{n-2} \] 当\(n\)足够大时,\(t\)分布近似于\(N(0,1)\)分布 \[ t_{1-\alpha}(n)=-t_\alpha(n) \] 设\(U\sim\chi^2(n_1),V\sim\chi^2(n_2)\),且\(U,V\)独立,则称随机变量 \[ F=\frac{U/n_1}{V/n_2} \] 服从自由度为\((n_1,n_2)\)的\(F\)分布,记为\(F\sim F(n_1,n_2)\) \[ \frac 1F\sim F(n_2,n_1) \]
\[ F_{1-\alpha}(n_1,n_2)=\frac 1{F_\alpha(n_2,n_1)} \]
设总体\(X\)(不管服从什么分布)的均值为\(\mu\),方差为\(\sigma^2\),\(X_1,X_2,\dots,X_n\)是来自\(X\)的一个样本,\(\overline X,S^2\)分别是样本均值和样本方差,则有 \[ E(\overline X)=\mu,\quad D(\overline X)=\sigma^2/n,\quad E(S^2)=\sigma^2 \] 设\(X_1,X_2,\dots,X_n\)是来自总体\(N(\mu,\sigma^2)\)的样本,\(\overline X,S^2\)分别是样本均值和样本方差,则有 \[ \overline{X}\sim N(\mu,\sigma^2/n) \]
\[ \frac{\overline X-\mu}{\sigma/\sqrt n}\sim N(0,1) \]
\[ \frac{\sum_{i=1}^n(X_i-\mu)^2}{\sigma^2}\sim\chi^2(n) \]
\[ \frac{\sum_{i=1}^n(X_i-\overline X)^2}{\sigma^2}=\frac{(n-1)S^2}{\sigma^2}\sim \chi^2(n-1) \]
\(\overline X\)与\(S^2\)相互独立 \[ \frac{\overline X-\mu}{S/\sqrt n}\sim t(n-1) \] 设\(X_1,X_2,\dots,X_{n_1}\)与\(Y_1,Y_2,\dots,Y_{n_2}\)分别是来自总体\(N(\mu_1,\sigma_1^2),N(\mu_2,\sigma_2^2)\)的样本,\(\overline X,\overline Y,S_1^2,S_2^2\)分别是这两个样本的样本均值和样本方差,则有 \[ \frac{(\overline X-\overline Y)-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\sim N(0,1) \]
\[ \frac{(\overline X-\overline Y)-(\mu_1-\mu_2)}{S_\omega\sqrt{\frac1{n_1}+\frac1{n_2}}}\sim t(n_1+n_2-2),\quad S_\omega^2=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2} \]
\[ \frac{\sum_{i=1}^{n}(X_i-\overline X)/n_1\sigma_1^2}{\sum_{j=1}^{n}(Y_j-\overline Y)/n_2\sigma_2^2}=\frac{S_1^2/S_2^2}{\sigma_1^2/\sigma_2^2}\sim F(n_1-1,n_2-1) \]
\[ \frac{\sum_{i=1}^{n}(X_i-\mu_1)/n_1\sigma_1^2}{\sum_{j=1}^{n}(Y_j-\mu_2)/n_2\sigma_2^2}\sim F(n_1,n_2) \]
第七章
矩估计:
计算总体矩 \[ \mu_l=E(X^l)=\int_{-\infty}^{+\infty}x^lf(x,\theta_1,\theta_2,\dots,\theta_k)\mathop{}\!\mathrm{d}x \]
取样\(X_1,X_2,\dots,X_n\)
计算样本矩 \[ A_l=\frac 1n\sum_{i=1}^nX_i^l \]
令\(A_l=E(X_i^l)\),解方程组
解得\(\hat \theta\)
极大似然估计:
写出极大似然函数 \[ L(\theta)=L(x_1,x_2,\dots,x_n;\theta_1,\theta_2,\dots,\theta_k)=\prod_{i=1}^nf(x_i;\theta_1,\theta_2,\dots,\theta_k) \]
求\(\ln L(x_1,x_2,\dots,x_n;\theta_1,\theta_2,\dots,\theta_k)\)
对\(k\)个参数,令 \[ \frac{\partial}{\partial\theta_t}\ln L(x_1,x_2,\dots,x_n;\theta_1,\theta_2,\dots,\theta_k)=0 \]
解方程组
估计量的评选标准:
- 无偏性:\(E(\hat\theta)=\theta\),称\(\hat\theta\)为\(\theta\)的无偏估计量
- 有效性:\(D(\hat\theta_1)\leq D(\hat\theta_2)\),称\(\hat\theta_1\)比\(\hat\theta_2\)有效
区间估计:
- 求未知参数\(\theta\)的点估计\(\hat \theta\)
- 选择枢轴量\(T=T(x;\theta)\),\(T\)的分布参数均为已知
- 对于给定的置信水平\(1-\alpha\),有\(P\{a<W<b\}=1-\alpha\),找到\(a,b\),为\(W\)对应的分位点
- 解得\(\hat\theta_1,\hat\theta_2\)满足\(P\{\hat\theta_1<\theta<\hat\theta_2\}=1-\alpha\)
常用的区间估计:
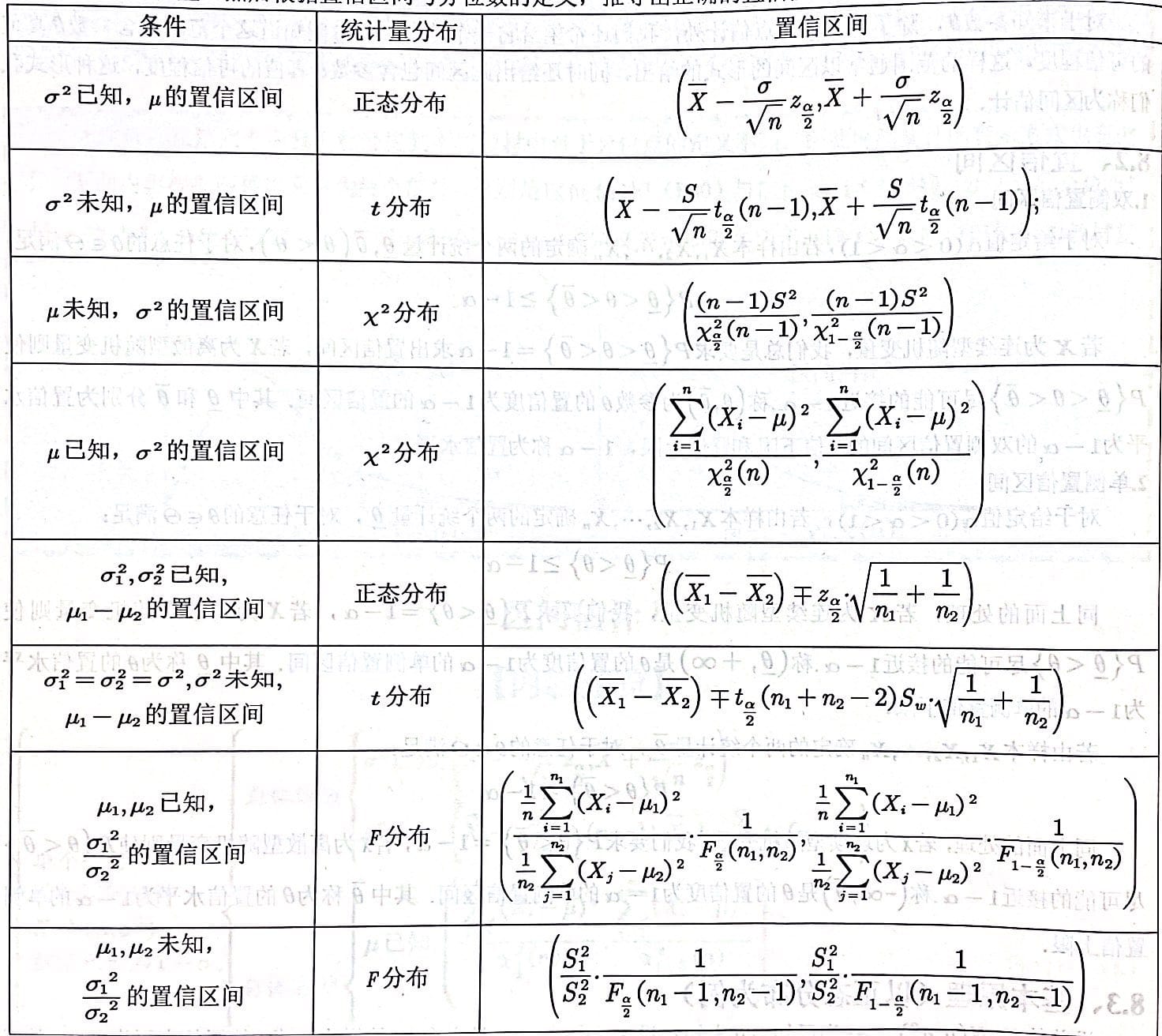
第八章
第一类错误:\(H_0\)实际为真,但拒绝\(H_0\),“弃真”
第二类错误:\(H_0\)实际为假,但接受\(H_0\),“取伪”
假设检验:
- 提出原假设\(H_0\)和备择假设\(H_1\)
- 给定显著性水平\(\alpha\)和样本容量\(n\)
- 确定检验统计量以及拒绝域
- 根据样本观察值计算
- 与拒绝域比较,做出决策
常用的假设检验:


检验两个正态总体\(\mu_1-\mu_2\)之前,先检验\(\sigma_1^2=\sigma_2^2\)
第九章
方差分析:
\[ T_{\cdot j}=\sum_{i=1}^{n_j}X_{ij}\quad T_{\cdot\cdot}=\sum_{j=1}^s\sum_{i=1}^{n_j}X_{ij} \]
\[ \begin{align*}& S_T=\sum_{j=1}^s\sum_{i=1}^{n_j}X_{ij}^2-\frac{T_{\cdot\cdot}^2}n \\ & S_A=\sum_{j=1}^s\frac{T_{\cdot j}^2}{n_j}-\frac{T_{\cdot\cdot}^2}n \\ & S_E=S_T-S_A\end{align*} \]
方差来源 平方和 自由度 均方 \(F\)比 因素\(A\) \(S_A\) \(s-1\) \(\overline{S_A}=\frac{S_A}{s-1}\) \(F=\frac{\overline{S_A}}{\overline{S_E}}\) 误差\(E\) \(S_E\) \(n-s\) \(\overline{S_E}=\frac{S_E}{n-s}\) 总和\(T\) \(S_T\) \(n-1\) \[ \hat{\sigma^2}=\frac{S_E}{n-s}\quad \hat\mu=\overline X\quad \hat{\mu_j}=\overline{X_{\cdot j}}\quad \hat{\delta_j}=\overline{X_{\cdot j}}-\overline X \]
\(\mu_j-\mu_k=\delta_j-\delta_k\)的区间估计,置信区间为 \[ \left(\overline{X_{\cdot j}}-\overline{X_{\cdot k}}\pm t_{\frac\alpha2}(n-s)\sqrt{\overline S_E\left(\frac1{n_j}+\frac1{n_k}\right)}\right) \]
一元线性回归:
\[ \begin{align*} & S_{xx}=\sum_{i=1}^{n}x_i^2-\frac1n\left(\sum_{i=1}^nx_i\right)^2 \\ & S_{yy}=\sum_{i=1}^{n}y_i^2-\frac1n\left(\sum_{i=1}^ny_i\right)^2 \\ & S_{xy}=\sum_{i=1}^{n}x_iy_i-\frac1n\left(\sum_{i=1}^nx_i\right)\left(\sum_{i=1}^ny_i\right) \end{align*} \]
\[ \begin{align*} & \hat b=\frac{S_{xy}}{S_{xx}} \\ & \hat a=\frac 1n\sum_{i=1}^{n}y_i-\left(\frac 1n\sum_{i=1}^nx_i\right)\hat b \end{align*} \]
检验假设\(H_0:b=0\quad H_1:b\not=0\)
F 检验法 \[ U=\frac{S_{xy}^2}{S_{xx}}\quad Q_e=S_{yy}-U \]
方差来源 平方和 自由度 \(F\)比 回归 \(U\) \(1\) \(F=\frac{U}{Q_e/(n-2)}\) 残差 \(Q_e\) \(n-2\) 总和 \(S_{yy}=U+Q_e\) 拒绝域\(F>F_{1-\alpha}(1,n-2)\)
概率论与数理统计公式