快速傅里叶变换

定义

快速傅里叶变换（Fast Fourier Transform，FFT）用于在\(O(n\log n)\)时间内求解多项式乘法。

有关概念

1. 虚数初步：人教数学 A 版选修 2-2 第三章；

2. 单位根：

   \(n\)次单位根指满足\(z^n=1\)的复数，这样的数总共有\(n\)个，分别为\(\omega_n^k=e^{\frac{2\pi ik}{n}},k=0,1,\ldots n-1\)；

   根据欧拉公式\(e^{ik}=\cos(k)+i\sin(k)\)，故\(\omega_n^k=\cos(\frac{2\pi ik}{n})+i\sin(\frac{2\pi ik}{n})\)；

   几何意义上，\(n\)次单位根均匀分布在复平面的单位圆上，在\(n=8\)时分布如下：

   

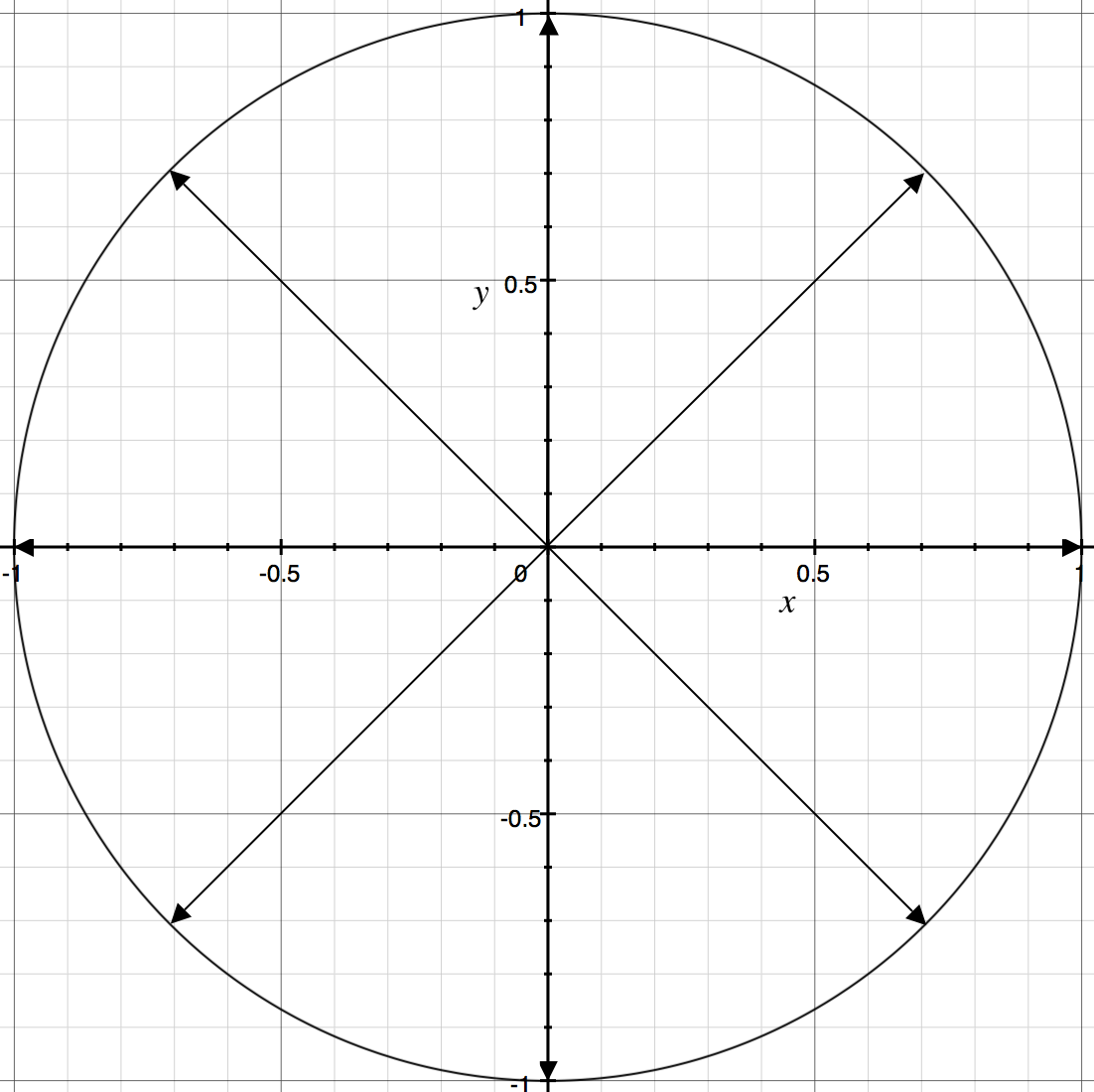
3. 多项式的表示方法：

   系数表达：如多项式\(2x^4+x^2+3x\)可以被表示为向量\(\vec{a}=(3,1,0,2)\)；

   点值表达：对于给定的\(n+1\)个不同的点，可以唯一确定一个\(n\)次多项式函数，一个多项式有无数种点值表达，将点值表达转换为系数表达的过程叫做插值，常用的有 拉格朗日插值法；

4. 多项式乘法：

   给定两个多项式\(A(x),B(x)\)：

   \[A(x)=\sum_{i=0}^n a_ix^i\]

   \[B(x)=\sum_{i=0}^n b_ix^i\]

   相乘得到\(C(x)\)：

   \[C(x)=\sum_{j+k=i,0\leq j,k\leq n} a_jb_kx^i\]

   系数表达求解的复杂度为\(O(n^2)\)，但是点值表达如果采样点相同，即如果\(A(x)\)和\(B(x)\)点值表达是横坐标对应相同的\(n+1\)个点，就可以直接相乘，求解复杂度为\(O(n)\)。

DFT 和 IDFT

离散傅里叶变换（Discrete Fourier Transform, DFT）可将系数表达转换为点值表达；

对于多项式\(A(x)=\sum_{i=0}^{n-1} a_ix^i\)的系数向量\(\vec{a}=(a_0,a_1,\ldots,a_{n-1}\)，其 DFT 定义为点值向量\(\vec{y}=A(\omega_n^0),A(\omega_n^1),\ldots,A(\omega_n^{n-1})\)。

IDFT（Inverse Discrete Fourier Transform）是 DFT 的逆，用于将点值表达转换为系数表达，即求解系数向量\(\vec{a}\)，给出方程组：

\[\left \{ \begin{array}{ccccccccc}&a_0(\omega_n^0)^0&+&a_1(\omega_n^0)^1&+&\ldots&+&a_{n-1}(\omega_n^0)^{n-1}&=&A(\omega_n^0)&\\&a_0(\omega_n^1)^0&+&a_1(\omega_n^1)^1&+&\ldots&+&a_{n-1}(\omega_n^1)^{n-1}&=&A(\omega_n^1)&\\&\vdots&&\vdots&&\vdots&&\vdots&&\vdots&\\&a_0(\omega_n^{n-1})^0&+&a_1(\omega_n^{n-1})^1&+&\ldots&+&a_{n-1}(\omega_n^{n-1})^{n-1}&=&A(\omega_n^{n-1})&\end{array} \right.\]

矩阵形式：

\[\begin{bmatrix} &(\omega_n^0)^0&(\omega_n^0)^1&\ldots&(\omega_n^0)^{n-1}&\\ &(\omega_n^1)^0&(\omega_n^1)^1&\ldots&(\omega_n^1)^{n-1}&\\ &\vdots&\vdots&\vdots&\vdots&\\ &(\omega_n^{n-1})^0&(\omega_n^{n-1})^1&\ldots&(\omega_n^{n-1})^{n-1}&\\ \end{bmatrix} \begin{bmatrix} a_0\\a_1\\ \vdots\\a_{n-1}\end{bmatrix} =\begin{bmatrix} A(\omega_n^0)\\A(\omega_n^1)\\ \vdots\\A(\omega_n^{n-1})\end{bmatrix}\]

设：

\[V=\begin{bmatrix} &(\omega_n^0)^0&(\omega_n^0)^1&\ldots&(\omega_n^0)^{n-1}&\\ &(\omega_n^1)^0&(\omega_n^1)^1&\ldots&(\omega_n^1)^{n-1}&\\ &\vdots&\vdots&\vdots&\vdots&\\ &(\omega_n^{n-1})^0&(\omega_n^{n-1})^1&\ldots&(\omega_n^{n-1})^{n-1}&\\ \end{bmatrix}\quad D=\begin{bmatrix} &(\omega_n^0)^0&(\omega_n^0)^1&\ldots&(\omega_n^0)^{n-1}&\\ &(\omega_n^{-1})^0&(\omega_n^{-1})^1&\ldots&(\omega_n^{-1})^{n-1}&\\ &\vdots&\vdots&\vdots&\vdots&\\ &(\omega_n^{-(n-1)})^0&(\omega_n^{-(n-1)})^1&\ldots&(\omega_n^{-(n-1)})^{n-1}&\\ \end{bmatrix} \quad E=V\cdot D\]

即\(e_{ij}=\sum_{k=0}^{n-1} v_{ik}d_{kj}=\sum_{k=0}^{n-1} \omega_n^{ik}\omega_n^{-kj}=\sum_{k=0}^{n-1} \omega_n^{(i-j)k}\)；

当\(i=j\)时，\(e_{ij}=n\)；

当\(i\not=j\)时，\(e_{ij}=\sum_{k=0}^{n-1} \omega_n^{(i-j)k}=\sum_{k=0}^{n-1} (\omega_n^{i-j})^k=\frac{1-(\omega_n^{i-j})^n}{1-\omega_n^{i-j}}=0\)；

故\(E\)矩阵在乘法中可看做数\(n\)；

故\(V^{-1}=\frac 1n D\)，乘入原等式：

\[\begin{bmatrix} a_0\\a_1\\ \vdots\\a_{n-1}\end{bmatrix} =\frac 1n \begin{bmatrix} &(\omega_n^0)^0&(\omega_n^0)^1&\ldots&(\omega_n^0)^{n-1}&\\ &(\omega_n^{-1})^0&(\omega_n^{-1})^1&\ldots&(\omega_n^{-1})^{n-1}&\\ &\vdots&\vdots&\vdots&\vdots&\\ &(\omega_n^{-(n-1)})^0&(\omega_n^{-(n-1)})^1&\ldots&(\omega_n^{-(n-1)})^{n-1}&\\ \end{bmatrix} \begin{bmatrix} A(\omega_n^0)\\A(\omega_n^1)\\ \vdots\\A(\omega_n^{n-1})\end{bmatrix} \]

于是，IDFT 和 DFT 的过程相同，只需要把\(\omega_n^i\)换成\(\omega_n^{-i}\)，再乘\(\frac 1n\)即可。

FFT

递归实现

思路与简单证明

至此为止，求 DFT 和 IDFT 的复杂度还是\(O(n^2)\)，于是我们可以利用单位根的几个性质来优化复杂度：

1. 消去引理：对于非负整数\(n,d,k\)，有\(\omega_{dn}^{dk}=\omega_n^k\)；

   证明：\(\omega_{dn}^{dk}=e^{\frac{2\pi idk}{dn}}=e^{\frac{2\pi ik}{n}}=\omega_n^k\)；

2. 折半引理：对于正偶数\(n\)，有\((\omega_n^{k+\frac{n}{2}})^2=(\omega_n^{k})^2\)；

   证明：由于\((\omega_n^\frac{n}{2})^2=\omega_n^n=1\)，故\(\omega_n^\frac{n}{2}=\pm 1\)，又\(\omega_n^\frac{n}{2}\not=\omega_n^n\)，故\(\omega_n^\frac{n}{2}=-1\)；

   \(\omega_n^{k+\frac{n}{2}}=\omega_n^{k}\omega_n^{\frac{n}{2}}=-\omega_n^{k}\)；

FFT 采用分治的思想，将原多项式\(A(x)\)分成两个多项式\(A^{[0]}(x),A^{[1]}(x)\)：

\[ A^{[0]}(x)=a_0+a_2x+a_4x^2+\ldots+a_{n-2}x^{\frac n2-1}\\ A^{[1]}(x)=a_1+a_3x+a_5x^2+\ldots+a_{n-1}x^{\frac n2-1} \]

可得\(A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)\)；

这时，根据消去引理，\((\omega_n^k)^2=\omega_n^{2k}=\omega_{\frac n2}{k}\)，故求\(A^{[0]}(x^2)\)和\(A^{[1]}(x^2)\)只需要代入\(\frac n2\)次单位根即可，使得代入的值也可以减半；

具体来说，\(A(\omega_n^k)=A^{[0]}((\omega_n^k)^2)+\omega_n^kA^{[1]}((\omega_n^k)^2)=A^{[0]}(\omega_{\frac n2}^k)+\omega_n^kA^{[1]}(\omega_{\frac n2}^k)\)

又根据折半引理，\(A(\omega_n^{k+\frac{n}{2}})=A(-\omega_n^{k})=A^{[0]}(\omega_{\frac n2}^k)-\omega_n^kA^{[1]}(\omega_{\frac n2}^k)\)

于是可以递归执行，复杂度优化到\(O(n\log n)\)，边界条件为\(n=1\)；

注意执行 FFT 之前先将次数\(n\)补齐到\(2\)的整数次幂。

实现

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<complex>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long LL;
typedef double db;
typedef complex<double> cp;
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-')f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+ch-'0'; ch=getchar(); }
    return x*f;
}
const int MAXN=3e5+10;
int n,m;
cp x[MAXN],y[MAXN];
void FFT(int n,cp *a,int flag)
{
    if(n==1)return;
    cp a0[(n>>1)+1],a1[(n>>1)+1];
    cp omega_n(cos(2*M_PI/n),sin(flag*2*M_PI/n)),omega(1,0);
    for(int i=0;i<(n>>1);++i)a0[i]=a[i<<1],a1[i]=a[i<<1|1];
    FFT(n>>1,a0,flag);
    FFT(n>>1,a1,flag);
    for(int i=0;i<(n>>1);++i)
    {
        a[i]=a0[i]+omega*a1[i];
        a[i+(n>>1)]=a0[i]-omega*a1[i];
        omega*=omega_n;
    }
    if(flag==-1)
        for(int i=0;i<n;++i)
            x[i]=int(x[i].real()/n+0.5);
    return;
}
int main()
{
    n=read();m=read();
    for(int i=0;i<=n;++i)x[i]=read();
    for(int i=0;i<=m;++i)y[i]=read();
    m+=n;n=1;
    while(n<=m)n<<=1;
    FFT(n,x,1);
    FFT(n,y,1);
    for(int i=0;i<n;++i)x[i]=x[i]*y[i];
    FFT(n,x,-1);
    for(int i=0;i<=m;++i)printf("%d ",(int)x[i].real());
    puts("");
    return 0;
}

迭代实现

思路与简单证明

考虑递归时的奇偶分组情况，如图（图中数字为系数下标）：

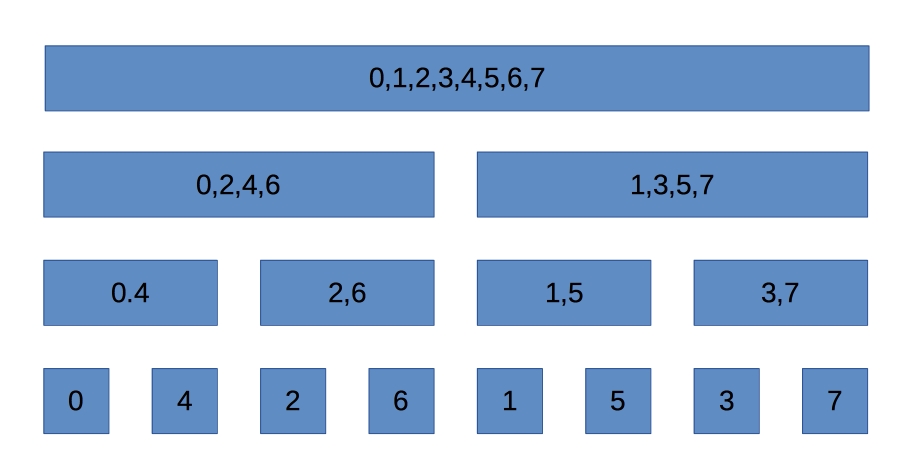
观察叶子节点中下标的排列情况，用二进制表示它们：

0	1	2	3	4	5	6	7
000	001	010	011	100	101	110	111
0	4	2	6	1	5	3	7
000	100	010	110	001	101	011	111

可以发现改变顺序后的排列是原排列每个数的二进制位逆序置换，如果我们知道了当前位置应该填的数，可以用类似于加法进位的方法求出下一个位置应该填的数：

从最高位开始，循环执行：检查当前位，若为\(0\)，将其置为\(1\)并退出循环；否则将其置为\(0\)，并检查低位；

求得当前位置的应有的下标后，可以与对应位置的数交换，因为二进制位逆序置换的数是一一对应的，所以每个数至多只会被交换一次；

以上过程被称为雷德算法。在求得最终排列后，就可以简单地循环执行，从小到大把数组分段操作即可。

实现

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<complex>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long LL;
typedef double db;
typedef complex<double> cp;
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-')f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+ch-'0'; ch=getchar(); }
    return x*f;
}
const int MAXN=3e5+10;
const db PI=acos(-1);
int n,m;
cp x[MAXN],y[MAXN];
void rader(int n,cp *x)
{
    for(int i=0,j=0;i<n;++i)
    {
        if(i<j)swap(x[i],x[j]);
        int k=n>>1;
        while((j^=k)<k)k>>=1;
    }
    return;
}
void FFT(int n,cp *x,int flag)
{
    rader(n,x);
    for(int len=2;len<=n;len<<=1)
    {
        cp omega_n(cos(flag*2*PI/len),sin(flag*2*PI/len));
        for(int i=0;i<n;i+=len)
        {
            cp omega(1,0);
            for(int j=i;j<i+(len>>1);++j)
            {
                cp t1=x[j],t2=omega*x[j+(len>>1)];
                x[j]=t1+t2;
                x[j+(len>>1)]=t1-t2;
                omega*=omega_n;
            }
        }
    }
    if(flag==-1)
        for(int i=0;i<n;++i)
            x[i]=int(x[i].real()/n+0.5);
    return;
}
int main()
{
    n=read();m=read();
    for(int i=0;i<=n;++i)x[i]=cp(read(),0);
    for(int i=0;i<=m;++i)y[i]=cp(read(),0);
    m+=n;n=1;
    while(n<=m)n<<=1;
    FFT(n,x,1);
    FFT(n,y,1);
    for(int i=0;i<n;++i)x[i]=x[i]*y[i];
    FFT(n,x,-1);
    for(int i=0;i<=m;++i)printf("%d ",(int)x[i].real());
    puts("");
    return 0;
}