1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
| #include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int MAXN=2000000,INF=0x3f3f3f3f;
int n,m,nn,head[MAXN],d[MAXN],cnt;
bool vis[MAXN];
struct edge
{
int v,next,val;
}e[MAXN*3];
void addedge(int x,int y,int z)
{
e[++cnt]=(edge){y,head[x],z};
head[x]=cnt;
return;
}
void inedge()
{
int x,cnt;
for(int i=1;i<=m-1;i++)
{
scanf("%d",&x);
addedge(0,i,x);addedge(i,0,x);
}
cnt=(m-1)*2;
for(int i=2;i<n;i++)
{
for(int j=1;j<=m-1;j++)
{
cnt++;
scanf("%d",&x);
addedge(cnt,cnt-m+1,x);addedge(cnt-m+1,cnt,x);
}
cnt+=(m-1);
}
for(int i=1;i<=m-1;i++)
{
scanf("%d",&x);
addedge(nn,nn-m+i,x);addedge(nn-m+i,nn,x);
}
cnt=m;
for(int i=1;i<=n-1;i++)
{
scanf("%d",&x);
addedge(cnt,nn,x);addedge(nn,cnt,x);
for(int j=2;j<m;j++)
{
cnt++;
scanf("%d",&x);
addedge(cnt,cnt-m,x);addedge(cnt-m,cnt,x);
}
scanf("%d",&x);
addedge(0,cnt-m+1,x);addedge(cnt-m+1,0,x);
cnt+=m;
}
cnt=0;
for(int i=1;i<=n-1;i++)
{
for(int j=1;j<=m-1;j++)
{
cnt++;
scanf("%d",&x);
addedge(cnt,cnt+m-1,x);addedge(cnt+m-1,cnt,x);
}
cnt+=(m-1);
}
return;
}
void SPFA()
{
queue<int>q;
q.push(0);
vis[0]=true;
while(!q.empty())
{
int u=q.front();q.pop();
vis[u]=false;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].v;
if(d[u]+e[i].val<d[v])
{
d[v]=d[u]+e[i].val;
if(!vis[v])
{
q.push(v);
vis[v]=true;
}
}
}
}
return;
}
int main()
{
scanf("%d%d",&n,&m);
if(n==1)
{
int x,ans=INF;
for(int i=1;i<=m-1;i++)
{
scanf("%d",&x);
ans=min(ans,x);
}
printf("%d\n",ans==INF?0:ans);
return 0;
}
else if(m==1)
{
int x,ans=INF;
for(int i=1;i<=n-1;i++)
{
scanf("%d",&x);
ans=min(ans,x);
}
printf("%d\n",ans==INF?0:ans);
return 0;
}
nn=(n-1)*(m-1)*2+1;
inedge();
for(int i=1;i<=nn;i++)d[i]=INF;
SPFA();
printf("%d\n",d[nn]);
return 0;
}
|
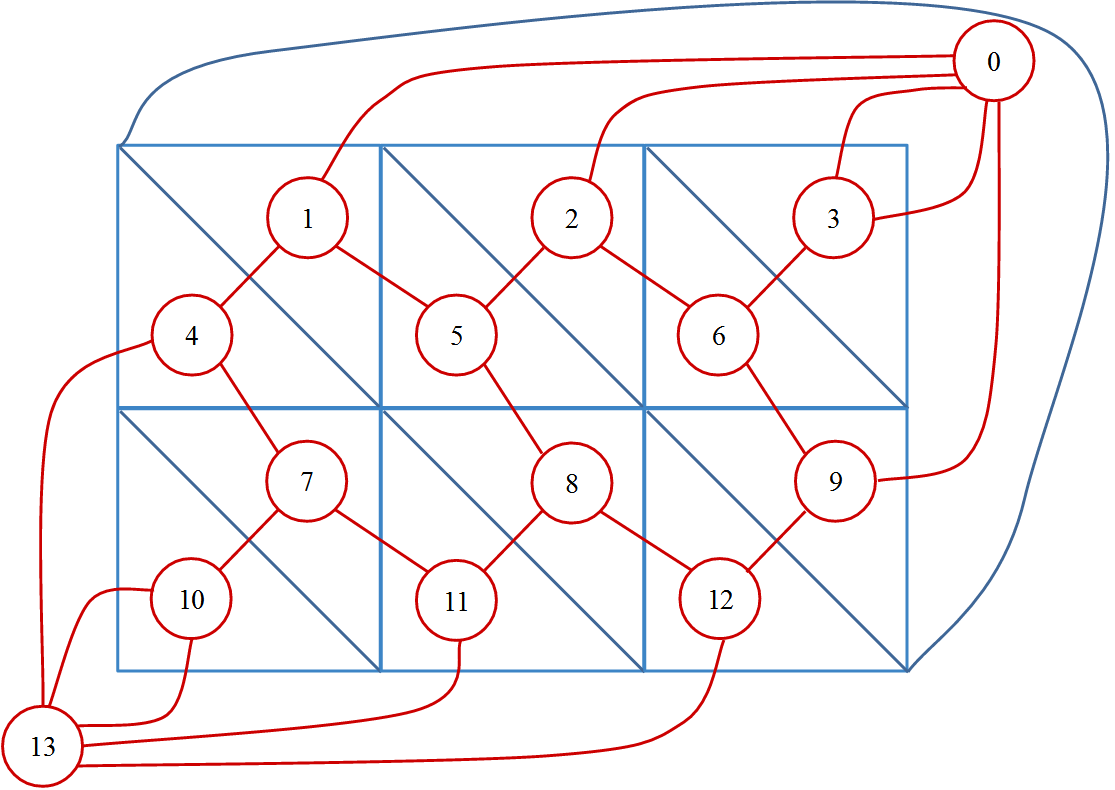
 对偶图\(G'\)
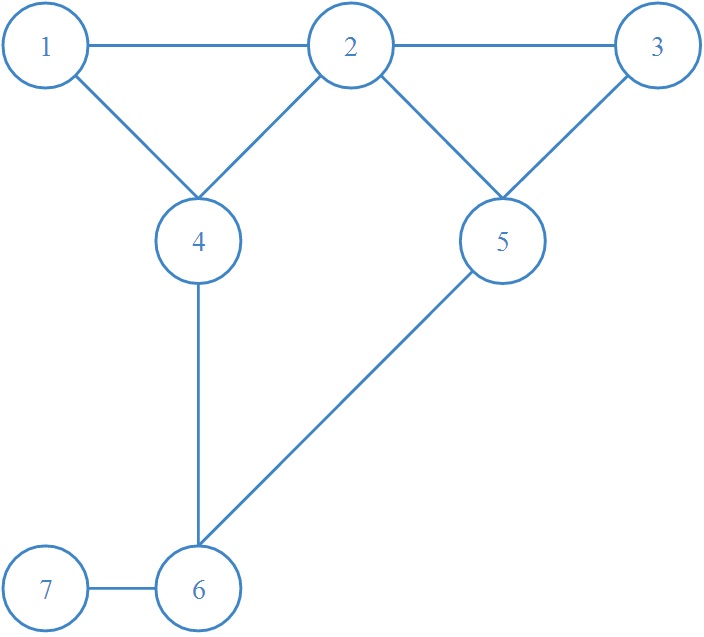
对偶图\(G'\) 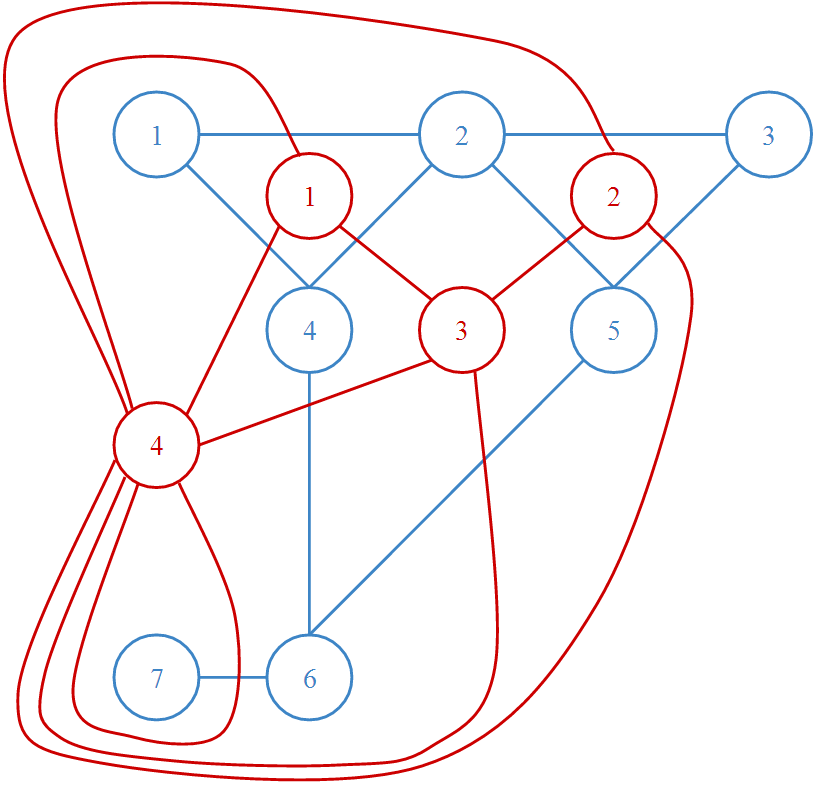 S-T
平面图:图中的一个点为源点\(S\),另一个点为汇点\(T\),且\(S\)和\(T\)都在图中无界面的边界上。
S-T
平面图:图中的一个点为源点\(S\),另一个点为汇点\(T\),且\(S\)和\(T\)都在图中无界面的边界上。